
分析 (Ⅰ)由题意设出直线l的方程,联立直线方程与椭圆方程,化为关于x的一元二次方程后由判别式大于0求得k的取值范围;
(Ⅱ)设出P、Q的坐标,利用根与系数的关系得到P、Q的横坐标的和与积,结合以PQ为直径的圆经过点E(1,0),由$\overrightarrow{PE}•\overrightarrow{QE}=0$求得k值,则直线方程可求.
解答 解:(Ⅰ)由题意可设直线l的方程为y=kx+2,
联立$\left\{\begin{array}{l}{y=kx+2}\\{\frac{{x}^{2}}{3}+{y}^{2}=1}\end{array}\right.$,得(1+3k2)x2+12kx+9=0,
由△=(12k)2-36(1+3k2)=36k2-36>0,
解得k<-1或k>1.
∴k的取值范围为(-∞,-1)∪(1,+∞);
(Ⅱ)设P(x1,y1),Q(x2,y2),
则由(Ⅰ)得:${x}_{1}+{x}_{2}=\frac{-12k}{1+3{k}^{2}},{x}_{1}{x}_{2}=\frac{9}{1+3{k}^{2}}$,
又E(1,0),
∴$\overrightarrow{PE}=(1-{x}_{1},-{y}_{1}),\overrightarrow{QE}=(1-{x}_{2},-{y}_{2})$,
由题意可知,$\overrightarrow{PE}•\overrightarrow{QE}=(1-{x}_{1},-{y}_{1})•(1-{x}_{2},-{y}_{2})$
=1-x1-x2+x1x2+(kx1+2)(kx2+2)=(1+k2)x1x2+(2k-1)(x1+x2)+5
=$(1+{k}^{2})•\frac{9}{1+3{k}^{2}}-(2k-1)•\frac{12k}{1+3{k}^{2}}+5$=$\frac{12k+14}{1+3{k}^{2}}=0$,
解得:k=-$\frac{7}{6}$,满足k<-1.
∴直线l的方程为y=-$\frac{7}{6}x+2$,即7x+6y-12=0.
点评 本题考查椭圆的简单性质,考查了直线与圆锥曲线位置关系的应用,体现了“设而不求”的解题思想方法,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
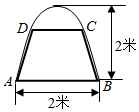 如图,有一块抛物线形钢板,其下口宽为2米,高为2米.计划将此钢板切割成等腰梯形的形状,下底AB是抛物线的下口,上底CD的端点在抛物线上.
如图,有一块抛物线形钢板,其下口宽为2米,高为2米.计划将此钢板切割成等腰梯形的形状,下底AB是抛物线的下口,上底CD的端点在抛物线上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 设全集U={1,2,3,4,5,6},集合A={1,2,4},B={1,3,5},则下列Venn图中阴影部分表示的集合是( )
设全集U={1,2,3,4,5,6},集合A={1,2,4},B={1,3,5},则下列Venn图中阴影部分表示的集合是( )| A. | {1} | B. | {2,4} | C. | {3,5} | D. | {2,3,4,5} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com