
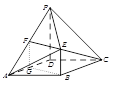
【题目】如图,四边形![]() 是菱形,
是菱形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
(![]() )求证:
)求证: ![]() 平面
平面![]() .
.
(![]() )求证:平面
)求证:平面![]() 平面
平面![]() .
.
(![]() )求三棱锥
)求三棱锥![]() 的体积.
的体积.

【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】试题分析:(Ⅰ)要证线面平行,就要证线线平行,由线面平行的性质定理知平行线是过![]() 的平面
的平面![]() 与平面
与平面![]() 的交线,由已知取
的交线,由已知取![]() 的中点
的中点![]() ,可证
,可证![]() 与
与![]() 平行且相等,从而有
平行且相等,从而有![]() ;(Ⅱ)要证面面垂直,一般先证线面垂直,由(Ⅰ)的证明过程及已知的垂直可知应证
;(Ⅱ)要证面面垂直,一般先证线面垂直,由(Ⅰ)的证明过程及已知的垂直可知应证![]() 平面
平面![]() ,而且易证(证
,而且易证(证![]() 平面
平面![]() );(Ⅲ)由(Ⅱ)知
);(Ⅲ)由(Ⅱ)知![]()
![]() .
.
试题解析:
(Ⅰ)取![]() 中点
中点![]() ,连接
,连接![]()
因为点![]() 为
为![]() 的中点,
的中点,
所以![]() 且
且![]()
又![]() ,且
,且![]() ,
,
所以![]()
所以四边形![]() 为平行四边形.
为平行四边形.
所以![]()
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)连接![]() .
.
因为四边形![]() 为菱形,
为菱形, ![]() ,所以
,所以![]() 为等边三角形.
为等边三角形.
因为![]() 为
为![]() 中点,所以
中点,所以![]() ,
,
又因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() ,
,
又![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
又![]() 所以
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
法二:因为四边形![]() 为菱形,
为菱形, ![]() ,所以
,所以![]() 为等边三角形.
为等边三角形.
因为![]() 为
为![]() 中点,所以
中点,所以![]() ,
,
又因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ,
,
又平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
又![]() 所以
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(Ⅲ)因为![]() ,
,
![]() , 所以
, 所以![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】定义:对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数![]() ,试判断
,试判断![]() 是否为定义域
是否为定义域![]() 上的“局部奇函数”?若是,求出所有满足
上的“局部奇函数”?若是,求出所有满足![]() 的
的![]() 的值;若不是,请说明事由.
的值;若不是,请说明事由.
(2)若![]() 是定义在区间
是定义在区间![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围.
的取值范围.
(3)若![]() 为定义域
为定义域![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC是直角三角形,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M. 
(1)求证:O、B、D、E四点共圆;
(2)求证:2DE2=DMAC+DMAB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 过焦点
过焦点![]() 交抛物线于
交抛物线于![]() 两点,
两点, ![]() ,点
,点![]() 的纵坐标为
的纵坐标为![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)若点![]() 是抛物线
是抛物线![]() 位于曲线
位于曲线![]() (
(![]() 为坐标原点)上一点,求
为坐标原点)上一点,求![]() 的最大面积.
的最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足f(2+x)=f(2﹣x),其图象开口向上,顶点为A,与x轴交于点B(﹣1,0)和C点,且△ABC的面积为18.
(1)求此二次函数的解析式;
(2)若方程f(x)=m(x﹣1)在区间[0,1]有解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校课题组为了研究学生的数学成绩和物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(百分制)如表所示:
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
若数学成绩90分(含90分)以上为优秀,物理成绩85(含85分)以上为优秀.有多少把握认为学生的数学成绩与物理成绩之间有关系( )
A.99.5%
B.99.9%
C.97.5%
D.95%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,直角梯形ABCD中,∠ABC=90°,AB=BC=2AD=4,点E、F分别是AB、CD的中点,点G在EF上,沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF,如图2.
(1)当AG+GC最小时,求证:BD⊥CG;
(2)当2VB﹣ADGE=VD﹣GBCF时,求二面角D﹣BG﹣C平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C所对的边分别为a、b、c,f (x)=sin(2x﹣A) (x∈R),函数f(x)的图象关于点( ![]() ,0)对称.
,0)对称.
(1)当x∈(0, ![]() )时,求f (x)的值域;
)时,求f (x)的值域;
(2)若a=7且sinB+sinC= ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com