
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 设l1,l2,l3,l4四条直线每两条都相交,且任三条都不交于一点,l1∩l2=A,l1∩l3=B,l3∩l4=C,l2∩l4=D,由平面的基本性质及推论推导出A,B,C,D四点共面,由此能求出结果.
解答 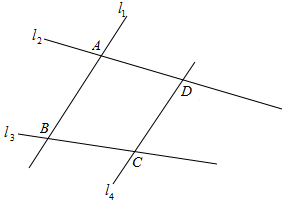 解:如图,l1,l2,l3,l4四条直线每两条都相交,且任三条都不交于一点,
解:如图,l1,l2,l3,l4四条直线每两条都相交,且任三条都不交于一点,
l1∩l2=A,l1∩l3=B,l3∩l4=C,l2∩l4=D,
∴l1和l2确定一个平面,设为α,
∵A,B∈l1,A,D∈l2,∴A,B,D三点共面于α,
l3,l4确定一个平面,设为β,
∵B,C∈l3,C,D∈l4,
∴B,C,D三点共面于β,
同理,A,B,C共面,A,D,C共面,
∵l1与l4相交,A,B∈l1,C,D∈l4,∴A,B,C,D四点共面,
∴四条直线每两条都相交,且任三条都不交于一点,它们可确定的平面个数为1个.
故选:A.
点评 本题考查平面的个数的确定,是基础题,解题时要认真审题,注意平面的基本性质及推论的合理运用.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:解答题
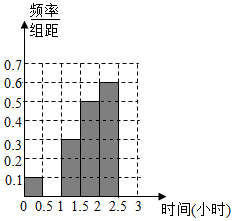 微信是现代生活进行信息交流的重要工具,随机对使用微信的60人进行了统计,得到如下数据统计表,每天使用微信时间在两小时以上的人被定义为“微信达人”,不超过2两小时的人被定义为“非微信达人”,己知“非微信达人”与“微信达人”人数比恰为3:2.
微信是现代生活进行信息交流的重要工具,随机对使用微信的60人进行了统计,得到如下数据统计表,每天使用微信时间在两小时以上的人被定义为“微信达人”,不超过2两小时的人被定义为“非微信达人”,己知“非微信达人”与“微信达人”人数比恰为3:2.| 使用微信时间(单位:小时) | 频数 | 频率 |
| (0,0.5] | 3 | 0.05 |
| (0.5,1] | x | p |
| (1,1.5] | 9 | 0.15 |
| (1.5,2] | 15 | 0.25 |
| (2,2.5] | 18 | 0.30 |
| (2.5,3] | y | q |
| 合计 | 60 | 1.00 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,5] | B. | [$\frac{\sqrt{29}}{3}$,$\sqrt{26}$] | C. | [$\sqrt{5}$,$\sqrt{26}$] | D. | [$\frac{\sqrt{2}}{2}$,$\sqrt{26}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com