
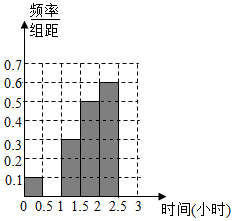
 �����ִ����������Ϣ��������Ҫ���ߣ������ʹ���ŵ�60�˽�����ͳ�ƣ��õ���������ͳ�Ʊ���ÿ��ʹ����ʱ������Сʱ���ϵ��˱�����Ϊ���Ŵ��ˡ���������2��Сʱ���˱�����Ϊ�����Ŵ��ˡ�����֪�����Ŵ��ˡ��롰�Ŵ��ˡ�������ǡΪ3��2��
�����ִ����������Ϣ��������Ҫ���ߣ������ʹ���ŵ�60�˽�����ͳ�ƣ��õ���������ͳ�Ʊ���ÿ��ʹ����ʱ������Сʱ���ϵ��˱�����Ϊ���Ŵ��ˡ���������2��Сʱ���˱�����Ϊ�����Ŵ��ˡ�����֪�����Ŵ��ˡ��롰�Ŵ��ˡ�������ǡΪ3��2��| ʹ����ʱ�䣨��λ��Сʱ�� | Ƶ�� | Ƶ�� |
| ��0��0.5] | 3 | 0.05 |
| ��0.5��1] | x | p |
| ��1��1.5] | 9 | 0.15 |
| ��1.5��2] | 15 | 0.25 |
| ��2��2.5] | 18 | 0.30 |
| ��2.5��3] | y | q |
| �ϼ� | 60 | 1.00 |
���� ��1�����ݷֲ�ֱ��ͼ��Ƶ�ʷֲ��������ʣ��г������飬��ȷ��x��y��p��q��ֵ������ȫ���ʷֲ�ֱ��ͼ��
��2���÷ֲ�����ķ���������ѡȡ10�ˣ������С��������ˡ���4�ˣ������������ˡ���6�ˣ��εĿ���ȡֵΪ0��1��2��3���ֱ������Ӧ�ĸ��ʣ��ɴ�������εķֲ��к���ѧ������
���  �⣺��1���������⣬��
�⣺��1���������⣬��
$\left\{\begin{array}{l}{3+x+9+15+18+y=60}\\{\frac{18+y}{3+x+9+15}=\frac{2}{3}}\end{array}\right.$��
���x=9��y=6��
��p=0.15��q=0.10��
��ȫƵ�ʷֲ�ͼ����ͼ��ʾ��
��2���÷ֲ�����ķ���������ѡȡ10�ˣ������С��������ˡ���10��$\frac{2}{5}$=4�ˣ������������ˡ���10��$\frac{3}{5}$=6�ˣ�
��εĿ���ȡֵΪ0��1��2��3��
P����=0��=$\frac{{C}_{4}^{0}{C}_{6}^{3}}{{C}_{10}^{3}}$=$\frac{1}{6}$��
P����=1��=$\frac{{C}_{4}^{1}{C}_{6}^{2}}{{C}_{10}^{3}}$=$\frac{1}{2}$��
P����=2��=$\frac{{C}_{4}^{2}{C}_{6}^{1}}{{C}_{10}^{3}}$=$\frac{3}{10}$��
P����=3��=$\frac{{C}_{4}^{3}{C}_{6}^{0}}{{C}_{10}^{3}}$=$\frac{1}{30}$��
��εķֲ���Ϊ��
| �� | 0 | 1 | 2 | 3 |
| P | $\frac{1}{6}$ | $\frac{1}{2}$ | $\frac{3}{10}$ | $\frac{1}{30}$ |
���� ���⿼���ͼ�����ֲ���������ʡ���ɢ����������ֲ����Լ���ѧ�����Ȼ���֪ʶ���������ø���ͳ��֪ʶ�����ʵ����������������ݴ���������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
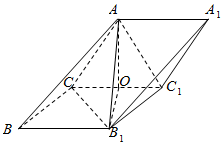 ��ͼ����������ABC-A1B1C1�У�AC=AC1=B1C=B1C1=2��AC��AC1��B1C��B1C1��OΪCC1���е㣮
��ͼ����������ABC-A1B1C1�У�AC=AC1=B1C=B1C1=2��AC��AC1��B1C��B1C1��OΪCC1���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�-$\sqrt{3}$���ȣ�$\sqrt{3}$��+�ޣ� | B�� | ��-$\sqrt{3}$��-1���ȣ�1��$\sqrt{3}$�� | C�� | ��-$\sqrt{3}$��$\sqrt{3}$�� | D�� | ��-�ޣ�-1���ȣ�1��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com