
分析 (1)利用函数的对称轴为x=-$\frac{a}{2}$,函数在(-$\frac{a}{2}$,+∞)上单调递增,即可证明结论;
(2)①根据函数f(x)的解析式,分别将x=1,2,3代入求得f(1),f(3),f(2),进而求得f(1)+f(3)-2f(2);
②“至少有一个不小于”的反面情况较简单,比较方便证明,故从反面进行证明,用反证法.
解答 证明:(1)函数的对称轴为x=-$\frac{a}{2}$,函数在(-$\frac{a}{2}$,+∞)上单调递增.
∵a2+$\frac{5}{4}$-(-$\frac{a}{2}$+1)=(a+$\frac{1}{2}$)2≥0,
∴a2+$\frac{5}{4}$≥-$\frac{a}{2}$+1
∴f(-$\frac{a}{2}$+1)≤f(a2+$\frac{5}{4}$);
(2)①∵f(x)=x2+ax+b,
∴f(1)=1+a+b,f(2)=4+2a+b,f(3)=9+3a+b
∴f(1)+f(3)-2f(2)=(1+a+b)+(9+3a+b)-2(4+2a+b)=2;
②假设|f(1)|,|f(2)|,|f(3)|都小于$\frac{1}{2}$,
则:|f(1)|<$\frac{1}{2}$,|f(2)|<$\frac{1}{2}$,|f(3)|<$\frac{1}{2}$,
即有-$\frac{1}{2}$<f(1)<$\frac{1}{2}$,-$\frac{1}{2}$<f(2)<$\frac{1}{2}$,-$\frac{1}{2}$<f(3)<$\frac{1}{2}$,
∴-2<f(1)+f(3)-2f(2)<2
由(1)可知f(1)+f(3)-2f(2)=2,
与-2<f(1)+f(3)-2f(2)<2矛盾,
∴假设不成立,即原命题成立.
点评 反证法是一种从反面的角度思考问题的证明方法,体现的原则是正难则反.反证法的基本思想:否定结论就会导致矛盾,证题模式可以简要的概括为“否定→推理→否定”.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
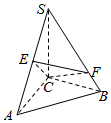 直线SC⊥面ABC,AB⊥BC,且AB=BC=1,SA=2,E为SA中点,F为点C在线BS上的射影.
直线SC⊥面ABC,AB⊥BC,且AB=BC=1,SA=2,E为SA中点,F为点C在线BS上的射影.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
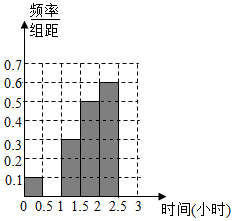 微信是现代生活进行信息交流的重要工具,随机对使用微信的60人进行了统计,得到如下数据统计表,每天使用微信时间在两小时以上的人被定义为“微信达人”,不超过2两小时的人被定义为“非微信达人”,己知“非微信达人”与“微信达人”人数比恰为3:2.
微信是现代生活进行信息交流的重要工具,随机对使用微信的60人进行了统计,得到如下数据统计表,每天使用微信时间在两小时以上的人被定义为“微信达人”,不超过2两小时的人被定义为“非微信达人”,己知“非微信达人”与“微信达人”人数比恰为3:2.| 使用微信时间(单位:小时) | 频数 | 频率 |
| (0,0.5] | 3 | 0.05 |
| (0.5,1] | x | p |
| (1,1.5] | 9 | 0.15 |
| (1.5,2] | 15 | 0.25 |
| (2,2.5] | 18 | 0.30 |
| (2.5,3] | y | q |
| 合计 | 60 | 1.00 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com