
分析 z=$cosθ+cos(θ+\frac{π}{2})i$=cosθ-isinθ,可得z的共轭复数$\overline z$=cosθ+isinθ,根据$θ∈(\frac{π}{2},π)$,可得cosθ,sinθ>0,即可得出.
解答 解:z=$cosθ+cos(θ+\frac{π}{2})i$=cosθ-isinθ,$θ∈(\frac{π}{2},π)$,
则z的共轭复数$\overline z$=cosθ+isinθ,
∵$θ∈(\frac{π}{2},π)$,∴cosθ,sinθ>0,
在复平面内对应第 一象限.
故答案为:一.
点评 本题考查了复数的几何意义、三角函数求值,考查了推理能力与计算能力,属于中档题.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:解答题
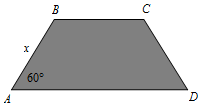 无锡市要建造一条防洪堤,其横断面为等腰梯形,腰与底边成角为60°(如图),考虑到防洪堤坚固性及石块用料等因素,设计基横断面要求面积为$6\sqrt{3}$平方米,且高度不低于$\sqrt{3}$米,记防洪堤横断面的腰长为x(米),外周长(梯形的上底线段BC与两腰长的和)为y(米).
无锡市要建造一条防洪堤,其横断面为等腰梯形,腰与底边成角为60°(如图),考虑到防洪堤坚固性及石块用料等因素,设计基横断面要求面积为$6\sqrt{3}$平方米,且高度不低于$\sqrt{3}$米,记防洪堤横断面的腰长为x(米),外周长(梯形的上底线段BC与两腰长的和)为y(米).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=3sin x | B. | y=3sin 2x | C. | y=3sin$\frac{1}{2}$x | D. | y=$\frac{1}{3}$sin 2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com