
| ������x����λ��Ԫ�� | 0 | 10 | 20 | 50 | 100 |
| �������������������y | 20 | 15 | 10 | 5 | 0 |
���� �����ݱ������������ݣ��õ�������꣬��ƽ��ֱ������ϵ�л���ɢ��ͼ�������������x�ͻ������������������y��ƽ�������õ��������ݵ��������ĵ㣬������С���˷�������Իع鷽�̵�ϵ���������������ĵ����a��ֵ��д�����Իع鷽�̣�
�����������֪���ع�ֱ�߷���-0.18x+16.48��200��5%�����x��ȡֵ��Χ��
��� �⣺����ɢ��ͼ��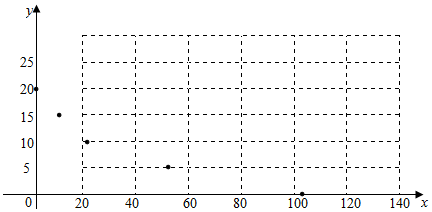
����2�֣�
��ɢ��ͼ���ж�����֮�为��� ����3�֣�
�ɱ������������ɵ�$\overline{x}$=$\frac{0+10+20+50+100}{5}$=36��$\overline{y}$=$\frac{20+15+10+5+0}{5}$=10��
��$\hat a=10-��-0.18����36=16.48$������7�֣�
�ʻع�ֱ�߷���Ϊ$\hat y=-0.18x+16.48$������8�֣�
������-0.18x+16.48��200��5%���ɵ�x��36������11�֣�
���ԣ�Ҫʹ���������߲�����5%���������������36Ԫ����12�֣�
���� ���⿼��ɢ��ͼ���������Իع鷽�̵��������������Իع鷽�̽���Ԥ�⣬���ڻ����⣮


 Ŀ�����ϵ�д�
Ŀ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -3+i | B�� | -1+3i | C�� | -3-i | D�� | -1-3i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -3 | B�� | -1 | C�� | 1 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com