练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设椭圆E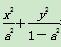：＝1的焦点在x轴上．

    (1)若椭圆E的焦距为1，求椭圆E的方程．

    (2)设F1，F2分别是椭圆的左、右焦点，P为椭圆E上的第一象限内的点，直线F2P交y轴于点Q，并且F1P⊥F1Q，证明：当a变化时，点P在某定直线上．

     


    由于F1P⊥F1Q，所以kF1P·kF1Q＝＝－1，化简得y＝x－(2a2－1)，①

    将①代入椭圆E的方程，由于点P(x0，y0)在第一象限，解得x0＝a2，y0＝1－a2，即点P在定直线x＋y＝1上．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知椭圆C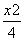：＋＝1的左、右焦点分别为F1，F2，椭圆C上点A满足AF2⊥F1F2.若点P是椭圆C上的动点，则·的最大值为(　　)

    A.                                  B.

    C.                                    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    方程(x－y)2＋(xy－1)2＝0表示的曲线是(　　)

    A．一条直线和一条双曲线                 B．两条直线

    C．两个点                               D．4条直线

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    经过椭圆＋y2＝1的一个焦点作倾斜角为45°的直线l，交椭圆于A，B两点．设O为坐标原点，则等于(　　)

    A．－3                                  B．－

    C．－或－3                            D．±

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知直线l：y＝x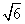＋，圆O：x2＋y2＝5，椭圆E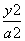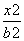：＋＝1(a>b>0)的离心率e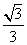＝，直线l被圆O截得的弦长与椭圆的短轴长相等．

    (1)求椭圆E的方程；

    (2)过圆O上任意一点P作椭圆E的两条切线，若切线都存在斜率，求证：两切线斜率之积为定值．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    执行如图所示的程序框图，若输出的结果是，则输入的a为(　　)

    A．5                                    B．6

    C．7                                    D．8

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图①是某市有关部门根据对当地干部的月收入情况调查后画出的样本频率分布直方图，已知图①中从左向右第一组的频数为4 000.在样本中记月收入在[1 000,1 500)，[1 500，2 000)，[2 000，2 500)，[2 500，3 000)，[3 000，3 500)，[3 500，4 000]的人数依次为A1，A2，…，A6.图②是统计图①中月工资收入在一定范围内的人数的程序框图，则样本的容量n＝________；图②输出的S＝________.(用数字作答)

     

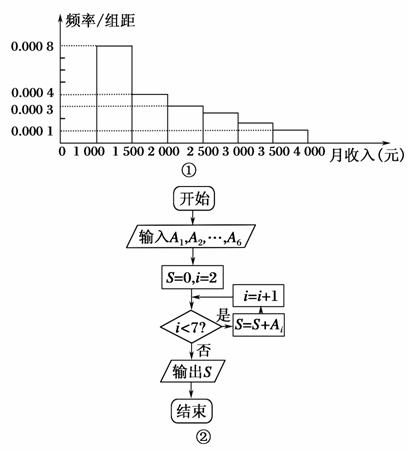
    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某单位200名职工的年龄分布情况如图，现要从中抽取40名职工作为样本．用系统抽样法将全体职工随机按1～200编号，并按编号顺序平均分为40组(1～5号，6～10号，…，196～200号)．若第5组抽出的号码为22，则第8组抽出的号码应是多少？若用分层抽样方法，则40岁以下年龄段应抽取多少人？

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若三角形的三边均为正整数，其中一边长为4，另外两边长分别为b、c，且满足b≤4≤c，则这样的三角形有(　　)

    A．10个                                 B．14个

    C．15个                                 D．21个

    查看答案和解析>>

    同步练习册答案