
| A. | 3 | B. | 4 | C. | 7 | D. | 9 |
分析 由题意可得:a2+a4+…+a2n=170.1+a3+a5+…+a2n+1=341,即a3+a5+…+a2n+1=340,可得q(a2+a4+…+a2n)=170q=340.解得q.再利用等比数列的求和公式即可得出.
解答 解:由题意可得:a2+a4+…+a2n=170.
1+a3+a5+…+a2n+1=341,即a3+a5+…+a2n+1=340,
∴q(a2+a4+…+a2n)=170q=340.
解得q=2.
∴$\frac{{4}^{n+1}-1}{4-1}$=341,解得n=4.
故选:B.
点评 本题考查了等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | c<a<b | C. | b<a<c | D. | a<c<b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
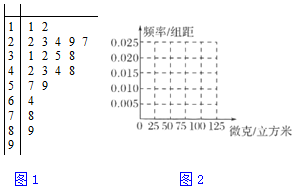
| 组别 | PM2.5浓度(微粒、立方米) | 频数(天) | 频率 |
| 第一组 | (0,25] | 5 | 0.25 |
| 第二组 | (25,50] | 10 | 0.5 |
| 第三组 | (50,75] | 3 | 0.15 |
| 第四组 | (75,100] | 2 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M?N | B. | N?M | C. | M∩N=ϕ | D. | M=N |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com