
Ζ÷Έω Α―œρΝΩΖ≈‘Ύ»ΐΫ«–Έ÷–Θ§ΗυΨίœρΝΩΒΡΦ–Ϋ«”κ»ΐΫ«–ΈΒΡΫ«ΒΡΙΊœΒΘ§ΉΣΜ·ΈΣΫβ»ΐΫ«–ΈΈ Χβ«σΫβΘ°
Ϋβ¥π 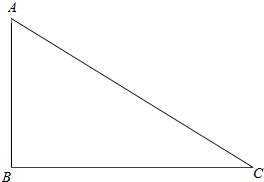 ΫβΘΚΓΏœρΝΩ$\overrightarrow{a}$Θ§$\overrightarrow{b}$Θ§$\overrightarrow{c}$¬ζΉψ$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=$\overrightarrow{0}$Θ§
ΫβΘΚΓΏœρΝΩ$\overrightarrow{a}$Θ§$\overrightarrow{b}$Θ§$\overrightarrow{c}$¬ζΉψ$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=$\overrightarrow{0}$Θ§
ΓύΝν$\overrightarrow{a}$=$\overrightarrow{BA}$Θ§$\overrightarrow{b}$=$\overrightarrow{AC}$Θ§$\overrightarrow{c}$=$\overrightarrow{CB}$Θ§
ΓΏ$\overrightarrow{a}$”κ$\overrightarrow{b}$ΒΡΦ–Ϋ«Β»”Ύ120ΓψΘ§$\overrightarrow{b}$”κ$\overrightarrow{c}$ΒΡΦ–Ϋ«Β»”Ύ15Γψ
ΓύΓœA=180Γψ-120Γψ=60ΓψΘ§ΓœC=180Γψ-150Γψ=30ΓψΘ§
Γύ»ΐΫ«–ΈΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§
$\frac{|AB|}{|BC|}$=tan30Γψ=$\frac{1}{\sqrt{3}}$Θ§
ΓΏ|BC|=|$\overrightarrow{c}$|=3Θ§
Γύ|AB|=$\sqrt{3}$Θ§
Ι ¥πΑΗΈΣΘΚ$\sqrt{3}$Θ°
ΒψΤά ±ΨΧβΩΦ≤ιœρΝΩ‘ΎΦΗΚΈ÷–ΒΡ”Π”ΟΓΔœρΝΩΒΡΡΘΘ§ ΐΝΩΜΐ±μ ΨΝΫΗωœρΝΩΒΡΦ–Ϋ«Θ§Ϋβ÷±Ϋ«»ΐΫ«–ΈΘ§―ß…ζ‘Υ”ΟΜ≠ΆΦ»ΖΕ®ΫβΨωΈ ΧβΒΡΖΫΖ®Θ§ τ”Ύ÷–ΒΒΧβΘ°


 ―ßΕχ”≈ νΤΎœΈΫ”ΡœΨ©¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ
―ßΕχ”≈ νΤΎœΈΫ”ΡœΨ©¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ Happy holidayΜΕά÷ΦΌΤΎ νΦΌΉς“ΒΙψΕΪ»ΥΟώ≥ωΑφ…γœΒΝ–¥πΑΗ
Happy holidayΜΕά÷ΦΌΤΎ νΦΌΉς“ΒΙψΕΪ»ΥΟώ≥ωΑφ…γœΒΝ–¥πΑΗ Ωλά÷ νΦΌ νΦΌΡήΝΠΉ‘≤β÷–Ές ιΨ÷œΒΝ–¥πΑΗ
Ωλά÷ νΦΌ νΦΌΡήΝΠΉ‘≤β÷–Ές ιΨ÷œΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | ΜΞ≥β | BΘ° | ≤ΜΜΞ≥β | CΘ° | œύΜΞΕάΝΔ | DΘ° | ≤ΜΕάΝΔ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com