
在棱长为1的正方体AC1中,E为AB的中点,点P为侧面BB1C1C内一动点(含边界),若动点P始终满足PE⊥BD1,则动点P的轨迹的长度为( )
A. B.
B. C.
C. D.
D.
科目:高中数学 来源:2014年高考数学人教版评估检测 第二章 函数、导数及其应用(解析版) 题型:解答题
(2014·孝感模拟)已知定义在区间[0,2]上的两个函数f(x)和g(x),其中f(x)=-x2+2ax+1+a2,g(x)=x- +
+ .
.
(1)求函数f(x)的最小值.
(2)对于?x1,x2∈[0,2],f(x1)>g(x2)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第三章 三角函数、解三角形(解析版) 题型:填空题
在△ABC中,2sin2 =
= sinA,sin(B-C)=2cosBsinC,则
sinA,sin(B-C)=2cosBsinC,则 =____________.
=____________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第七章 立体几何(解析版) 题型:解答题
已知等腰梯形PDCB中(如图),PB=3,DC=1,PD=BC= ,A为PB边上一点,且PA=1,将△PAD沿AD折起,使平面PAD⊥平面ABCD(如图).
,A为PB边上一点,且PA=1,将△PAD沿AD折起,使平面PAD⊥平面ABCD(如图).
(1 )证明:平面PAD⊥平面PCD.
)证明:平面PAD⊥平面PCD.
(2)试在棱PB上确定一点M,使截面AMC把几何体分成的两部分VPDCMA∶VMACB=2∶1.
(3)在M满足(2)的情况下,判断直线PD是否平行平面AMC.

查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第七章 立体几何(解析版) 题型:填空题
如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD 的中点,在此几何体中,给出下面四个结论:
的中点,在此几何体中,给出下面四个结论:

①直线BE与直线CF异面;
②直线BE与直线AF异面;
③直线EF∥平面PBC;
④平面BCE⊥平面PAD.
其中正确的有__________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第七章 立体几何(解析版) 题型:选择题
(2014·宜昌模拟)一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为( )

A.9 B.10 C.11 D.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 集合、常用逻辑用语、不等式、函数与导数(解析版) 题型:解答题
已知函数f(x)= ax3+(a-2)x+c的图象如图所示.
ax3+(a-2)x+c的图象如图所示.

(1)求函数y=f(x)的解析式;
(2)若g(x)= -2ln x在其定义域内为增函数,求实数k的取值范围.
-2ln x在其定义域内为增函数,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 集合、常用逻辑用语、不等式、函数与导数(解析版) 题型:选择题
“φ=π”是“曲线y=sin(2x+φ)过坐标原点”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 立体几何(解析版) 题型:选择题
已知等比数列{an},若存在两项am,an使得am·an=a32,则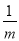 +
+ 的最小值为( )
的最小值为( )
A.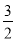 B.
B. C.
C.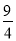 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com