
���� ����������֪���Ӽס��������и���ȡһ��С�鵽���Ϊ1�ź���ĸ���Ϊ$\frac{1}{3}$���鵽n�ź���ĸ���Ϊ$\frac{1}{n}$������������¼����ʼ��㹫ʽ���ɵó���
�����������֪����=1��2��3��4������������뻥���¼����ʼ��㹫ʽ����ѧ�������㹫ʽ���ɵó���
��� �⣺����������֪��$\frac{1}{3}��\frac{1}{n}$=$\frac{1}{12}$����n=4��
�����������֪����=1��2��3��4��
$P����=1��=\frac{1}{C_2^1}•\frac{C_2^1}{C_4^1}=\frac{1}{6}$��$P����=2��=\frac{C_1^1}{C_3^1}•\frac{C_2^1}{C_4^1}+\frac{C_1^1}{C_3^1}•\frac{C_2^1}{C_4^1}=\frac{1}{6}+\frac{1}{6}=\frac{1}{3}$��
$P����=3��=\frac{C_1^1}{C_3^1}•\frac{C_2^1}{C_4^1}+\frac{C_1^1}{C_3^1}•\frac{C_2^1}{C_4^1}=\frac{1}{6}+\frac{1}{6}=\frac{1}{3}$��
$P����=4��=\frac{1}{C_2^1}•\frac{C_2^1}{C_4^1}=\frac{1}{6}$��
$E��=1��\frac{1}{6}+2��\frac{1}{3}+3��\frac{1}{3}+4��\frac{1}{6}=\frac{5}{2}$��
���� ���⿼����������뻥���¼����ʼ��㹫ʽ����ѧ�������㹫ʽ��������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
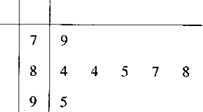
| A�� | 87��85 | B�� | 86��85 | C�� | 87��84 | D�� | 86��84 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | ������ | C�� | $\frac{��}{2}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com