Question

17．如图是一建筑物的三视图（单位：米），现需将其外壁用油漆刷一遍，若每平方米用漆α千克，则共需油漆的总量为（　　）

• A． （48+36π）α千克
• B． （39+24π）α千克
• C． （36+36π）α千克
• D． （36+30π）α千克

Answer 1

分析 根据三视图确定几何体的形状，求出一个几何体的表面积，然后求出需要的油漆数目即可．

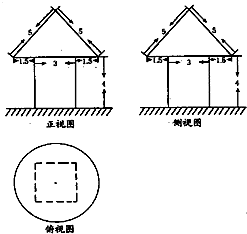
解答 解：建筑物是由一个底面半径为3、母线长为5的圆锥和
一个底面边长为3、高为4的长方体组成．                                                   
油漆粉刷部位有三部分组成：
一是圆锥的侧面（面积记为S₁）；
二是长方体的侧面（面积记为S₂）；
三是圆锥的底面除去一个边长为3的正方形（面积记为S₃）．
则S₁=π×3×5=15π（m²），S₂=4×3×4=48（m²），S₃=π×3²-3×3=9π-9（m²）
记油漆粉刷面积为S，则S=S₁+S₂+S₃=24π+39（m²）．      
记油漆重量为ykg，则y=（39+24π）a．
故选：B．

点评 本题考查的知识点是简单空间图象的三视图，其中根据已知中的视图分析出几何体的形状及棱长是解答的关键．