
分析 (Ⅰ)当a=1时,求得函数的导数,求出切线的斜率和切点坐标,由点斜式方程即可得到切线的方程;
(Ⅱ)转化已知条件为函数f(x)在[1,e]上的最小值[f(x)]min≤0,利用单调性,①a≥e-1时,②a≤0时,③0<a<e-1时,分别求解函数的最小值,推出所求a的范围;
(Ⅲ)化简g(x)=f(ax)-$\frac{a+1}{ax}$=ax-alnax,(a>0),求出导数,求得单调区间和极小值,令它小于0,求得a>e,再由x1=lnax1,x2=lnax2,相加,构造函数,求出最值,再由不等式的性质,即可得证.
解答 解:(Ⅰ)当a=1时,f(x)=x+$\frac{2}{x}$-lnx的导数为f′(x)=1-$\frac{2}{{x}^{2}}$-$\frac{1}{x}$,
曲线f(x)在x=1处的切线斜率为f′(1)=-2,
切点为(1,3),
即有切线方程为y-3=-2(x-1),即为2x+y-5=0;
(Ⅱ)由题意可知,在[1,e]上存在一点x0,使得f(x0)≤0,
即函数f(x)=x+$\frac{a+1}{x}$-alnx在[1,e]上的最小值[f(x)]min≤0.
由f(x)的导数f′(x)=1-$\frac{a+1}{{x}^{2}}$-$\frac{a}{x}$=$\frac{(x+1)(x-a-1)}{x}$,
①当a+1≥e,即a≥e-1时,f(x)在[1,e]上单调递减,
∴[f(x)]min=f(e)=e+$\frac{1+a}{e}$-a,
∴a≥$\frac{{e}^{2}+1}{e-1}$,
∵$\frac{{e}^{2}+1}{e-1}$>e-1,
∴a≥$\frac{{e}^{2}+1}{e-1}$;
②当a+1≤1,即a≤0时,f(x)在[1,e]上单调递增,
∴[f(x)]min=f(1)=1+1+a≤0,
∴a≤-2;
③当1<a+1<e,即0<a<e-1时,
∴[f(x)]min=f(1+a)=2+a-aln(1+a)≤0,
∵0<ln(1+a)<1,∴0<aln(1+a)<a,∴h(1+a)>2
此时不存在x0使h(x0)≤0成立.
综上可得所求a的范围是:a≥$\frac{{e}^{2}+1}{e-1}$,或a≤-2.
(Ⅲ)函数g(x)=f(ax)-$\frac{a+1}{ax}$=ax-alnax,(a>0),
g′(x)=a-a•$\frac{1}{x}$,当x>1时,g′(x)>0,g(x)递增,
当0<x<1时,g′(x)<0,g(x)递减.
即有x=1处g(x)取得极小值,也为最小值,且为a-alna,
g(x)有两个不同的零点,则有a-alna<0,解得a>e,
g(x)有两个不同的零点x1,x2,且0<x1<x2,
即x1=lnax1,x2=lnax2,相加可得x1+x2=lnax1+lnax2=ln(a2x1x2),
x1x2=$\frac{1}{{a}^{2}}$${e}^{{x}_{1}+{x}_{2}}$,
即有$\frac{2{x}_{1}{x}_{2}}{{x}_{1}+{x}_{2}}$=$\frac{\frac{2}{{a}^{2}}{e}^{{x}_{1}+{x}_{2}}}{{x}_{1}+{x}_{2}}$,令t=x1+x2,则h(t)=$\frac{{e}^{t}}{t}$的导数为$\frac{{e}^{t}(t-1)}{{t}^{2}}$,
当t>1时,h(t)递增,当0<t<1时,h(t)递减,即有t=1时,h(t)取得最小值,且为e,
有$\frac{2{x}_{1}{x}_{2}}{{x}_{1}+{x}_{2}}$<$\frac{2}{{e}^{2}}$•e=$\frac{2}{e}$<1,lna>1,
则有$\frac{2{x}_{1}{x}_{2}}{{x}_{1}+{x}_{2}}$<lna.
点评 本题考查函数的导数的综合应用,曲线的切线方程、函数的单调性以及函数的最值的应用,考查分析问题解决问题得到能力.


科目:高中数学 来源: 题型:选择题
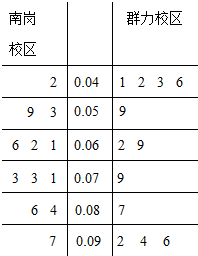 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据哈尔滨三中学生社团某日早6点至晚9点在南岗、群力两个校区附近的PM2.5监测点统计的数据(单位:毫克/立方米)列出的茎叶图,南岗、群力两个校区浓度的方差较小的是( )
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据哈尔滨三中学生社团某日早6点至晚9点在南岗、群力两个校区附近的PM2.5监测点统计的数据(单位:毫克/立方米)列出的茎叶图,南岗、群力两个校区浓度的方差较小的是( )| A. | 南岗校区 | B. | 群力校区 | ||
| C. | 南岗、群力两个校区相等 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
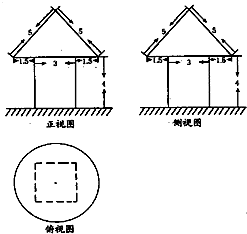
| A. | (48+36π)α千克 | B. | (39+24π)α千克 | C. | (36+36π)α千克 | D. | (36+30π)α千克 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
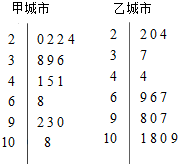 空气质量指数PM2.5 (单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
空气质量指数PM2.5 (单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:| PM2.5日均浓度 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 | >250 |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com