Question

4．空气质量指数PM2.5 （单位：μg/m³）表示每立方米空气中可入肺颗粒物的含量，这个值越高，就代表空气污染越严重：

PM2.5日均浓度	0～35	35～75	75～115	115～150	150～250	＞250
空气质量级别	一级	二级	三级	四级	五级	六级
空气质量类别	优	良	轻度污染	中度污染	重度污染	严重污染

甲、乙两城市2015年2月份中的15天对空气质量指数PM2.5进行监测，获得PM2.5日均浓度指数数据如茎叶图所示：
（Ⅰ）根据你所学的统计知识分别写出甲、乙两城市15天内空气质量的中位数，并分析两城市空气质量哪个较好？
（Ⅱ）王先生到乙地出差5天，已知该5天是空气质量最好的五天，王先生要在这5天中选择两天出去游玩，求这两天恰好有一天空气质量类别为优的概率．

Answer 1

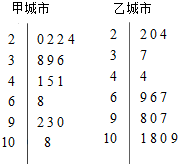
分析 （1）根据茎叶图的知识，以及中位数的定义即可求出们根据中位数即可判断甲地的空气质量要比乙地好；
（2）空气质量最好的五天中优的有3天，用A，B，C表示，良的有2天，用，D，E表示，王先生要在这5天中选择两天出去游玩，基本事件有10种，其中这两天恰好有一天空气质量类别为优共6种，根据概率公式计算即可．

解答 解：（1）中位数甲：41 乙：69，
甲地的空气质量要比乙地好，可以通过茎叶图中心位置、中位数、集中程度、个体差异等方面进行描述；
（2）空气质量最好的五天中优的有3天，用A，B，C表示，良的有2天，用，D，E表示，王先生要在这5天中选择两天出去游玩，基本事件有10种，分别为
AB，AC，AD，AE，BC，BD，BE，CD，CE，DE，其中这两天恰好有一天空气质量类别为优，有AD，AE，BD，BE，CD，CE，共6种，
故这两天恰好有一天空气质量类别为优的概率为$\frac{3}{5}$．

点评 本题考查茎叶图，等可能事件概率的求法，考查利用数学知识解决实际问题，属于基础题．