
分析 (1)设切点为(x0,y0),求出函数y=f(x+a)的导数,求得切线的斜率,解方程可得a=1;
(2)求出g(x)和h(x)的导数,运用韦达定理和函数的零点的定义,化简整理,构造函数,运用导数判断单调性,即可得到所求最小值.
解答 解:(1)由题意得,函数y=f(x+a)=ln(x+a)与直线y=x相切,
设切点为(x0,y0),$y'=f'(x+a)=\frac{1}{x+a}$,
∴${\left.{y'}\right|_{x={x_0}}}=\frac{1}{{{x_0}+a}}=1$,∴x0+a=1又有x0=ln(x0+a)
∴x0=0,a=1;
(2)$g(x)=lnx+\frac{1}{2}{x^2}-mx(m≥\frac{5}{2})$,h(x)=lnx-cx2-bx
由已知$g'(x)=\frac{{{x^2}-mx+1}}{x}=0$的两根为x1,x2,
当$m≥\frac{5}{2}$时方程x2-mx+1=0的△>0,
则x1+x2=m,x1x2=1,
又由x1,x2为h(x)=lnx-cx2-bx的零点可得$\left\{{\begin{array}{l}{ln{x_1}-cx_1^2-b{x_1}=0}\\{ln{x_2}-cx_2^2-b{x_2}=0}\end{array}}\right.$,
两式相减$ln\frac{x_1}{x_2}-c({x_1}+{x_2})({x_1}-{x_2})-b({x_1}-{x_2})=0$,可解得$b=\frac{{ln\frac{x_1}{x_2}}}{{{x_1}-{x_2}}}-c({x_1}+{x_2})$①
而$y=({x_1}-{x_2})h'(\frac{{{x_1}+{x_2}}}{2})$=(x1-x2)[$\frac{2}{{{x_1}+{x_2}}}-c({x_1}+{x_2})-b]$代入①式
可得y=$({x_1}-{x_2})(\frac{2}{{{x_1}+{x_2}}}-\frac{{ln\frac{x_1}{x_2}}}{{{x_1}-{x_2}}})$=$2\frac{{{x_1}-{x_2}}}{{{x_1}+{x_2}}}-ln\frac{x_1}{x_2}$=$2\frac{{\frac{x_1}{x_2}-1}}{{\frac{x_1}{x_2}+1}}-ln\frac{x_1}{x_2}$,
令$\frac{x_1}{x_2}=t$(0<t<1),由x1+x2=m,x1x2=1可得$t+\frac{1}{t}+2={m^2}$,则$t∈(0,\frac{1}{4}]$,
设函数$G(t)=2\frac{t-1}{t+1}-lnt$,而$G'(t)=\frac{{-{{(t-1)}^2}}}{{t{{(t+1)}^2}}}<0$,
则y=G(t)在$t∈(0,\frac{1}{4}]$单调递减,
所以$G{(t)_{min}}=G(\frac{1}{4})=-\frac{6}{5}+ln4$,
即$y=({x_1}-{x_2})h'(\frac{{{x_1}+{x_2}}}{2})$的最小值为$-\frac{6}{5}+ln4$.
点评 本题考查导数的运用:求切线的斜率、单调区间和最值,同时考查二次方程的韦达定理和函数的零点,考查运算求解能力,属于中档题.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
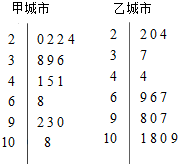 空气质量指数PM2.5 (单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
空气质量指数PM2.5 (单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:| PM2.5日均浓度 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 | >250 |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (-∞,0) | C. | (0,1] | D. | [0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com