
分析 先求出没有限制条件的种数为720种,
(Ⅰ)先安排甲,再安排乙,剩下的全排,根据概率公式计算即可,
(Ⅱ)先选2人放在甲乙之间,并捆绑在一起,看作一个复合元素,再和剩下的2人全排,根据概率公式计算即可,
解答 解:没有限制条件的种数为A66=720种,
(Ⅰ)先安排甲,再安排乙,剩下的全排,故有C21C31A44=144种,
根据概率公式,故甲在1或2跑道且乙不在5或6跑道的概率P=$\frac{144}{720}$=$\frac{1}{5}$,
(Ⅱ)先选2人放在甲乙之间,并捆绑在一起,看作一个复合元素,再和剩下的2人全排,故有A42A22A33=144种,
根据概率公式,故甲乙之间恰好间隔两人的概率P=$\frac{144}{720}$=$\frac{1}{5}$.
点评 本题考查古典概型的概率问题,关键是根据排列组合求出相应的种数,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图所示,几何体ABCDE中,△ABC为正三角形,CD⊥面ABC,BE∥CD,BC=CD=2BE.
如图所示,几何体ABCDE中,△ABC为正三角形,CD⊥面ABC,BE∥CD,BC=CD=2BE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
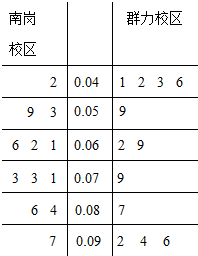 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据哈尔滨三中学生社团某日早6点至晚9点在南岗、群力两个校区附近的PM2.5监测点统计的数据(单位:毫克/立方米)列出的茎叶图,南岗、群力两个校区浓度的方差较小的是( )
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据哈尔滨三中学生社团某日早6点至晚9点在南岗、群力两个校区附近的PM2.5监测点统计的数据(单位:毫克/立方米)列出的茎叶图,南岗、群力两个校区浓度的方差较小的是( )| A. | 南岗校区 | B. | 群力校区 | ||
| C. | 南岗、群力两个校区相等 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2}{5}$i | B. | $\frac{2}{5}$i | C. | -$\frac{2}{5}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
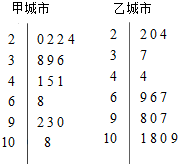 空气质量指数PM2.5 (单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
空气质量指数PM2.5 (单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:| PM2.5日均浓度 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 | >250 |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com