Question

7．如图所示，几何体ABCDE中，△ABC为正三角形，CD⊥面ABC，BE∥CD，BC=CD=2BE．
（Ⅰ）在线段AD上找一点F，使EF∥平面ABC，并证明；
（Ⅱ）求证：面ADE⊥面ACD．

Answer 1

分析 （Ⅰ）取线段AC中点M，连结BM，FM，EF，证明出四边形BEFM平行四边形，推断出EF∥BM，进而利用线面平行的判定定理证明出EF∥平面ABC；
（Ⅱ）利用线面垂直的判定定理证明出BM⊥面ACD，进而推断EF⊥面ACD，最后利用面面垂直的判定定理证明出结论

解答 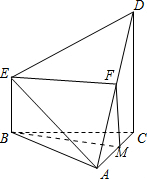解：（Ⅰ）
点F为线段AD中点，
证明如下：
取线段AC中点M，连结BM，FM，EF，
∵BE∥CD，BC=CD=2BE
则FM∥CD∥BE，且$FM=\frac{1}{2}CD=BE$，
所以四边形BEFM平行四边形，则EF∥BM，
又∵EF?平面ABC，BM⊆平面ABC，
∴EF∥平面ABC；
（Ⅱ）证明：∵△ABC为正三角形，
∴BM⊥AC，
∵CD⊥面ABC，BM⊆平面ABC，
∴CD⊥BM，
∵CD∩AC=C，
∴BM⊥面ACD，
∵EF∥BM，
∴EF⊥面ACD，
又EF⊆平面ADE，
∴面ADE⊥面ACD．

点评 本题主要考查了线面平行和面面垂直的判定定理的运用．考查了学生的一定的空间观察和想象能力．