练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．已知x＞0，则$2+3x+\frac{4}{x}$的最小值等于2+4$\sqrt{3}$．

    分析 根据基本不等式即可求出答案．

    解答 解：$2+3x+\frac{4}{x}$≥2+2$\sqrt{3x•\frac{4}{x}}$=2+4$\sqrt{3}$，当且仅当x=$\frac{2\sqrt{3}}{3}$时取等号，
    故最小值为$2+4\sqrt{3}$．
    故答案为：2+4$\sqrt{3}$

    点评 本题考查了基本不等式的应用，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    14．式子$lg4+2lg5+{4^{-\frac{1}{2}}}$的化简结果为$\frac{5}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

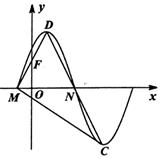    15．如图是函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜$\frac{π}{2}$）的部分图象，M，N是它与x轴的两个交点，D，C分别为它的最高点和最低点，点F（0，1）是线段MD的中点，三角形MDC的面积为$\frac{2π}{3}$．
    （Ⅰ）求函数f（x）的解析式；
    （Ⅱ）若f（x）-m＞0在$x∈[{-\frac{π}{36}，\frac{π}{36}}]$上恒成立，求m的取值范围；
    （Ⅲ）将函数y=f（x）的图象向左平移$\frac{π}{6}$个单位，再往上平移1个单位，得到函数y=g（x）的图象．求y=g（x）在区间[2009π，2017π]上的零点个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知a≥0，函数f （x）=（x2-2ax）ex，若f （x）在[-1，1]上是单调减函数，则a的取值范围是（　　）
    A．（0，$\frac{3}{4}$）B．（$\frac{1}{2}$，$\frac{3}{4}$）C．（0，$\frac{1}{2}$）D．[$\frac{3}{4}$，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．随机变量$ξ～B（n，\frac{1}{3}）$，且E（3ξ+2）=8，则n=6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．若等差数列{an}与等比数列{bn}中，若a1=b1＞0，a11=b11＞0，则a6，b6的大小关系为a6≥b6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

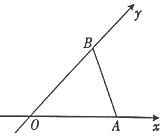    16．用斜二测画法画一个水平放置的平面图形的直观图为如图所示的等腰三角形，其中OA=OB=1，则原平面图形的面积为（　　）
    A．1B．$\sqrt{2}$C．$\frac{3}{2}$D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．直线l在平面α内，直线m平行于平面α，且与直线l异面，动点P在平面α上，且到直线l、m距离相等，则点P的轨迹为（　　）
    A．直线B．椭圆C．抛物线D．双曲线

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．设$\overrightarrow{a}$，$\overrightarrow{b}$是非零向量，则“$\overrightarrow{a}$，$\overrightarrow{b}$共线”是“|$\overrightarrow{a}$|+|$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$|”的（　　）
    A．充分而不必要条件B．必要而不充分条件
    C．充分必要条件D．既不充分也不必要条件

    查看答案和解析>>

    同步练习册答案