
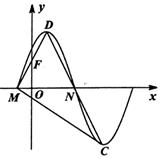
 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象,M,N是它与x轴的两个交点,D,C分别为它的最高点和最低点,点F(0,1)是线段MD的中点,三角形MDC的面积为$\frac{2π}{3}$.
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象,M,N是它与x轴的两个交点,D,C分别为它的最高点和最低点,点F(0,1)是线段MD的中点,三角形MDC的面积为$\frac{2π}{3}$.分析 (Ⅰ)由题意根据点F(0,1)是线段MD的中点,求得最高点和最低点的坐标,可得A的值,再根据三角形MDC的面积为$\frac{2π}{3}$,求得ω的值,再根据特殊点的坐标求得φ的值,可得函数f(x)的解析式,再利用正弦函数的单调性,求得f(x)的解析式.
(Ⅱ)若f(x)-m>0在$x∈[{-\frac{π}{36},\frac{π}{36}}]$上恒成立,求得f(x)的最小值,可得m的取值范围.
(Ⅲ)利用函数y=Asin(ωx+φ)的图象变换规律求得g(x)的解析式,再根据g(x)的周期性求得 y=g(x)在区间[2009π,2017π]上的零点个数.
解答 解:(Ⅰ)由点F(0,1)是线段MD的中点,可知A=2,三角形MDC的面积为$\frac{1}{2}×\frac{T}{2}×2×2=\frac{2π}{3}$,
所以$T=\frac{2π}{3},ω=\frac{2π}{T}=3$,设点D(x0,2),则M(-x0,0),
∴$4({x_0}-(-{x_0}))=\frac{2π}{3},{x_0}=\frac{π}{12}$,即$D(\frac{π}{12},2)$,所以$2sin(3×\frac{π}{12}+ϕ)=2$,
∵$0<ϕ<\frac{π}{2}$,∴$ϕ=\frac{π}{4}$,所以函数f(x)的解析式$f(x)=2sin(3x+\frac{π}{4})$
由$\frac{π}{2}+2kπ≤3x+\frac{π}{4}≤\frac{3π}{2}+2kπ(k∈Z)$得$\frac{π}{4}+2kπ≤3x≤\frac{5π}{4}+2kπ(k∈Z)$
得$\frac{π}{12}+\frac{2kπ}{3}≤x≤\frac{5π}{12}+\frac{2kπ}{3}(k∈Z)$,
所以函数f(x)的单调减区间为$[\frac{π}{12}+\frac{2kπ}{3},\frac{5π}{12}+\frac{2kπ}{3}](k∈Z)$.
(Ⅱ)因为不等式f(x)-m>0在$x∈[{-\frac{π}{36},\frac{π}{36}}]$上恒成立,
所以m<(f(x))min在$x∈[{-\frac{π}{36},\frac{π}{36}}]$,∵$x∈[{-\frac{π}{36},\frac{π}{36}}]$,∴$3x+\frac{π}{4}∈[{\frac{π}{6},\frac{π}{3}}].f{(x)_{min}}=2sin\frac{π}{6}=1$,即m<1.
(Ⅲ)依题意得$g(x)=f(x+\frac{π}{6})+1=2cos(3x+\frac{π}{4})+1$,
其最小正周期$T=\frac{2π}{3}$,由$2cos(3x+\frac{π}{4})+1=0$,得$cos(3x+\frac{π}{4})=-\frac{1}{2}$,
所以$3x+\frac{π}{4}=2kπ±\frac{2π}{3},k∈Z$,即$x=\frac{2kπ}{3}+\frac{5π}{36},k∈Z$或$x=\frac{2kπ}{3}-\frac{11π}{36},k∈Z$,
区间[2009π,2017π]的长度为12个周期,
若零点不在区间的端点,则每个周期有2个零点;
若零点在区间的端点,则仅在区间左或右端点处得一个区间含3个零点,其它区间仍是2个零点;
故当$2009π≠\frac{2kπ}{3}+\frac{5π}{36},k∈Z$且$2009π≠\frac{2kπ}{3}-\frac{11π}{36},k∈Z$,故有12×2=24个.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由特殊点的坐标求出ω 和φ的值;正弦函数的单调性、周期性、零点,函数y=Asin(ωx+φ)的图象变换规律,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | $(-∞,\frac{1}{2})$ | C. | $(0,\frac{1}{2})$ | D. | $(\frac{1}{2},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{4}{5}i$ | C. | $\frac{6}{5}$ | D. | $\frac{6}{5}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{7}}{3}$ | B. | $\frac{8}{3}$ | C. | $\frac{2\sqrt{19}}{3}$ | D. | $\frac{2\sqrt{13}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-y=0 | B. | x+y=0 | C. | x+2y-3=0 | D. | (x+1)2+(y-2)2=5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com