
| A. | $\frac{2\sqrt{7}}{3}$ | B. | $\frac{8}{3}$ | C. | $\frac{2\sqrt{19}}{3}$ | D. | $\frac{2\sqrt{13}}{3}$ |
分析 以A为原点,以AB所在的直线为x轴,建立如图所示的坐标系,根据向量的坐标运算可得y=$\sqrt{3}$(x-2),当直线y=$\sqrt{3}$(x-2)与直线BC相交时,此时
此时|$\overrightarrow{AP}$|最大,问题得以解决
解答 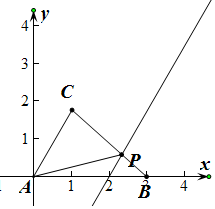 解:以A为原点,以AB所在的直线为x轴,建立如图所示的坐标系,
解:以A为原点,以AB所在的直线为x轴,建立如图所示的坐标系,
∵AB=3,AC=2,∠BAC=60°,
∴A(0,0),B(3,0),C(1,$\sqrt{3}$),
设点P为(x,y),0≤x≤2,0≤y≤$\sqrt{3}$,
∵$\overrightarrow{AP}=\frac{2}{3}\overrightarrow{AB}+λ\overrightarrow{AC}$,
∴(x,y)=$\frac{2}{3}$(3,0)+λ(1,$\sqrt{3}$)=(2+λ,$\sqrt{3}$λ),
∴$\left\{\begin{array}{l}{x=2+λ}\\{y=\sqrt{3}λ}\end{array}\right.$,
∴y=$\sqrt{3}$(x-2),①
直线BC的方程为y=-$\frac{\sqrt{3}}{2}$(x-3),②,
联立①②,解得$\left\{\begin{array}{l}{x=\frac{7}{3}}\\{y=\frac{\sqrt{3}}{3}}\end{array}\right.$,
此时|$\overrightarrow{AP}$|最大,
∴|AP|=$\sqrt{\frac{49}{9}+\frac{1}{3}}$=$\frac{2\sqrt{13}}{3}$,
故选:D.
点评 本题考查了向量在及几何中的应用,关键建立直角坐标系,考查了学生的数形结合的能力,属于中档题


科目:高中数学 来源: 题型:解答题
| 理财金额 | 1万元 | 2万元 | 3万元 |
| 乙理财相应金额的概率 | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{3}$ |
| 丙理财相应金额的概率 | $\frac{1}{2}$ | $\frac{1}{3}$ | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
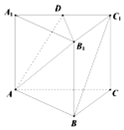 如图,在直三棱柱ABC-A1B1C1中,底面ABC为边长为2的正三角形,D是棱A1C1的中点,CC1=h(h>0).
如图,在直三棱柱ABC-A1B1C1中,底面ABC为边长为2的正三角形,D是棱A1C1的中点,CC1=h(h>0).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{3π}{4}$ | C. | π | D. | $\frac{3π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
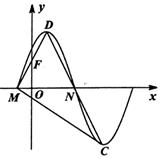 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象,M,N是它与x轴的两个交点,D,C分别为它的最高点和最低点,点F(0,1)是线段MD的中点,三角形MDC的面积为$\frac{2π}{3}$.
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象,M,N是它与x轴的两个交点,D,C分别为它的最高点和最低点,点F(0,1)是线段MD的中点,三角形MDC的面积为$\frac{2π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≥-2 | B. | a>2 | C. | 0<a<1 | D. | 1≤a<2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com