
����Ŀ��Ŀǰ���ɶ���B������ļƼ۱��ǣ�·��2km���ڣ���2km������8Ԫ��ȡ������2km���·�̰�1.9Ԫ/km��ȡ��������10km���·�������50%�ķ��շѣ�������Ϊ1.9����1+50%��=2.85Ԫ/km��������ʵ��Ҫ�Ƶȴ�ʱ�������ո���ȡ�����������ڼ���ʱ�����迼�ǣ�
��1�����˿ʹ��һ��B������ķ���f��x����Ԫ����ʾΪ�г�x��0��x��60����λ��km���ķֶκ�����
��2��ij�˿��г�Ϊ16km�������ȳ�һ��B�������ʻ8km��Ȼ���ٻ�����һ��B�������������г̣����ʣ����������Ƿ��ֻ��һ��B��������ȫ���г̸�ʡǮ��
���𰸡�
��1���⣺������ã�����f��x������·��x�ĺ���Ϊ��
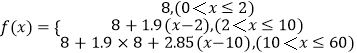
= 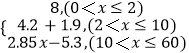
��2���⣺ֻ��һ�����ij���Ϊ��f��16��=2.85��16��5.3=40.3��Ԫ����
����2�����ij���Ϊ��2f��8��=2����4.2+1.9��8��=38.8��Ԫ����
��40.3��38.8��
��ó˿ͻ��˱�ֻ��һ������ʡǮ
����������1����ϸ���⣬�ɳɶ���B������ļƼ۱����ܹ��г��˿ʹ��һ��B������ķ���f��x����Ԫ����ʾΪ�г�x��0��x��60����λ��km���ķֶκ�������2��ֻ��һ�����ij���Ϊ��f��16��=2.85��16��5.3=40.3Ԫ������2�����ij���Ϊ��2f��8��=2����4.2+1.9��8��=38.8Ԫ���ɴ��ܵõ��ó˿ͻ��˱�ֻ��һ������ʡǮ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=loga�� ![]() +x��������a��1����
+x��������a��1����
��1���жϺ���y=f��x������ż�ԣ���˵�����ɣ�
��2���ж� ![]() ������m��n��R����m+n��0������������˵�����ɣ�
������m��n��R����m+n��0������������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����f��x�����溯�������ڣ�0��+�ޣ���������������f����3��=0����x��1��f��x����0�Ľ⼯�ǣ� ��
A.{x|��3��x��0��1��x��3}
B.{x|1��x��3}
C.{x|x��3��x����3}
D.{x|x����3��x��1}
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ƽ����һ����![]() ��������
��������![]() ��
��![]() ���ߵ�б��֮������
���ߵ�б��֮������![]() .
.
������![]() �Ĺ켣
�Ĺ켣![]() �ķ��̣�
�ķ��̣�
������ֱ��![]() ��
�� ![]() ��
��![]() ����켣
����켣![]() ����
����![]() ��
��![]() ���㣬�߶�
���㣬�߶�![]() �Ĵ�ֱƽ���߽�
�Ĵ�ֱƽ���߽�![]() ���ڵ�
���ڵ�![]() ����
����![]() �仯ʱ����
�仯ʱ����![]() ��������ֵ.
��������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����p������ ![]() =1��ʾ˫���ߣ�����q��x�ʣ�0��+�ޣ���x2��mx+4��0���������p��q�������⣬�ҽ���p��q��Ҳ�������⣬��m��ȡֵ��Χ��
=1��ʾ˫���ߣ�����q��x�ʣ�0��+�ޣ���x2��mx+4��0���������p��q�������⣬�ҽ���p��q��Ҳ�������⣬��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������
������![]() Ϊ��Ȼ�����ĵ���.
Ϊ��Ȼ�����ĵ���.
��1������![]() ��ͼ���ܷ���
��ͼ���ܷ���![]() �����У�������
�����У�������![]() �����У���ʵ��
�����У���ʵ��![]() ��ֵ��������˵�����ɣ�
��ֵ��������˵�����ɣ�
��2��������![]() ��
��![]() �ϵ�����������ʵ��
�ϵ�����������ʵ��![]() ��ȡ�����������ֵ.
��ȡ�����������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() �ĵ���
�ĵ���![]() �DZ߳�Ϊ2�������Σ�
�DZ߳�Ϊ2�������Σ� ![]() ����
����![]() ��
�� ![]() ����
����![]() ��
��
�����߶�![]() ���е�Ϊ
���е�Ϊ![]() ����ƽ��
����ƽ��![]() �ڹ���
�ڹ���![]() ��һ��ֱ����ƽ��
��һ��ֱ����ƽ��![]() ƽ�У�Ҫ������ͼ�ۼ�������Ҫ��֤����
ƽ�У�Ҫ������ͼ�ۼ�������Ҫ��֤����
������ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x3+ax2+bx+c������y=f��x���ڵ�x=0��������Ϊl��4x+y��5=0����x=��2ʱ��y=f��x���м�ֵ��
��1����a��b��c��ֵ��
��2����y=f��x����[��3��1]�ϵ����ֵ����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�༶����һ��֪ʶ����������Ϊ�����;��������Ρ��ֽ���������ɼ����÷־�Ϊ����������Ϊ100�֣�����ͳ�ƣ��Ƴ�����Ƶ�ʷֲ�����
�����������Σ� | Ƶ���������� | Ƶ�� |
[60��70�� | �� | 0.16 |
[70��80�� | 22 | �� |
[80��90�� | 14 | 0.28 |
[90��100] | �� | �� |
�� �� | 50 | 1 |
��1�����Ƶ�ʷֲ����еĿո��ڽ����ֱ��д����Ӧ�ո���ŵĴ𰸣���
��2�������������£��μӾ�����ÿλͬѧ���οڴ�4��С�⣬���2�������ֹ���⣬�����һ�Ƚ������ǰ�����ⶼ������Ͳ��ٴ�����⡣ijͬѧ���������ÿ�����Եĸ���![]() ��ֵǡ����Ƶ�ʷֲ����в�����80�ֵ�Ƶ�ʵ�ֵ��ͬ��
��ֵǡ����Ƶ�ʷֲ����в�����80�ֵ�Ƶ�ʵ�ֵ��ͬ��
�����ͬѧǡ�ô���4��������һ�Ƚ��ĸ��ʣ�
�ڼǸ�ͬѧ�����д������Ϊ![]() ����
����![]() �ķֲ��м���ѧ������
�ķֲ��м���ѧ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com