
【题目】某班级举行一次知识竞赛活动,活动分为初赛和决赛两个阶段。现将初赛答卷成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表.
分数(分数段) | 频数(人数) | 频率 |
[60,70) | ① | 0.16 |
[70,80) | 22 | ② |
[80,90) | 14 | 0.28 |
[90,100] | ③ | ④ |
合 计 | 50 | 1 |
(1)填充频率分布表中的空格(在解答中直接写出对应空格序号的答案);
(2)决赛规则如下:参加决赛的每位同学依次口答4道小题,答对2道题就终止答题,并获得一等奖。如果前三道题都答错,就不再答第四题。某同学进入决赛,每道题答对的概率![]() 的值恰好与频率分布表中不少于80分的频率的值相同.
的值恰好与频率分布表中不少于80分的频率的值相同.
①求该同学恰好答满4道题而获得一等奖的概率;
②记该同学决赛中答题个数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
【答案】(1)①8 ②0.44 ③6 ④0.12;(2)①0.1728;②见解析.
【解析】试题分析:(1)根据样本容量,频率和频数之间的关系得到要求的几个数据,注意第三个数据是用样本容量减去其他三个数得到;(2)①该同学恰好答满![]() 道题而获得一等奖,即前
道题而获得一等奖,即前![]() 道题中刚好答对
道题中刚好答对![]() 道,第
道,第![]() 道也能够答对才获得一等奖,根据相互独立事件的概率公式得到结果;②答对
道也能够答对才获得一等奖,根据相互独立事件的概率公式得到结果;②答对![]() 道题就终止答题,并获得一等奖,所以该同学答题个数为
道题就终止答题,并获得一等奖,所以该同学答题个数为![]() ,即
,即![]() ,结合变量对应的概率,写出分布列和期望.
,结合变量对应的概率,写出分布列和期望.
试题解析:(1)由图中数据知,样本容量为50,根据频率=![]() ,
,
①处=0.16×50=8;②处=![]() ;③处填:50﹣44=6;④处填:
;③处填:50﹣44=6;④处填:![]() .
.
故有:①8 ②0.44 ③6 ④0.12.
由(1),得![]()
①该同学恰好答满4道题而获得一等奖,即前3道题中刚好答对1道,
第4道也能够答对才获得一等奖,则有![]() ×0.4×0.62×0.4=0.1728.
×0.4×0.62×0.4=0.1728.
②由题设可知,该同学答题个数为2、3、4.即X=2、3、4,
![]()
![]()
![]()
| 2 | 3 | 4 |
| 0.16 | 0.408 | 0.432 |
分布列为:
![]() .
.


科目:高中数学 来源: 题型:
【题目】目前,成都市B档出租车的计价标准是:路程2km以内(含2km)按起步价8元收取,超过2km后的路程按1.9元/km收取,但超过10km后的路程需加收50%的返空费(即单价为1.9×(1+50%)=2.85元/km).(现实中要计等待时间且最终付费取整数,本题在计算时都不予考虑)
(1)将乘客搭乘一次B档出租车的费用f(x)(元)表示为行程x(0<x≤60,单位:km)的分段函数;
(2)某乘客行程为16km,他准备先乘一辆B档出租车行驶8km,然后再换乘另一辆B档出租车完成余下行程,请问:他这样做是否比只乘一辆B档出租车完成全部行程更省钱?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点(x,y)是区域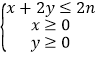 , (n∈N*)内的点,目标函数z=x+y,z的最大值记作zn . 若数列{an}的前n项和为Sn , a1=1,且点(Sn , an)在直线zn=x+y上.
, (n∈N*)内的点,目标函数z=x+y,z的最大值记作zn . 若数列{an}的前n项和为Sn , a1=1,且点(Sn , an)在直线zn=x+y上.
证明:数列{an﹣2}为等比数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学习兴趣小组开展“学生语文成绩与外语成绩的关系”的课题研究,考察该校高二年级800名学生上学期期末的语文和外语成绩,按是否优秀分类得结果:语文和外语成绩都优秀的有60人,语文成绩优秀但外语成绩不优秀的有140人,外语成绩优秀但语文成绩不优秀的有100人.
(Ⅰ)能否有![]() 的把握认为“该校学生语文成绩优秀与外语成绩是否优秀有关系”?
的把握认为“该校学生语文成绩优秀与外语成绩是否优秀有关系”?
(Ⅱ)将上述调查所得到的频率视为概率,从该校高二年级学生成绩中,有放回地随机抽取3名学生的成绩,记所抽取的成绩中,语文、外语两科成绩至少有一科优秀的人数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
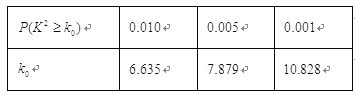
附:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的各项均为正数,且Sn= ![]() +
+ ![]() +…+
+…+ ![]() ,S2=
,S2= ![]() ,S3=
,S3= ![]() .设[x]表示不大于x的最大整数(如[2.10]=2,[0.9]=0).
.设[x]表示不大于x的最大整数(如[2.10]=2,[0.9]=0).
(1)试求数列{an}的通项;
(2)求T=[log21]+[log22]+[log23]+…+[log2( ![]() ﹣1)]+[log2(
﹣1)]+[log2( ![]() )]关于n的表达式.
)]关于n的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=ax2﹣2ax+b(a≠0)在闭区间[1,2]上有最大值0,最小值﹣1,则a,b的值为( )
A.a=1,b=0
B.a=﹣1,b=﹣1
C.a=1,b=0或a=﹣1,b=﹣1
D.以上答案均不正确
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com