练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．下列函数中，定义域为R的是（　　）
    A．y=$-\frac{{\sqrt{5}}}{e^x}$B．y=$\sqrt{x+1}$C．y=lnxD．y=x-1

    分析 根据函数成立的条件即可求函数的定义域．

    解答 解：A．函数的定义域是R，满足条件
    B．要使函数有意义，则x+1≥0，得x≥-1，即函数的定义域是[-1，+∞），不满足条件．
    C．要使函数有意义，则x＞0，即函数的定义域是（0，+∞），不满足条件．
    D．要使函数有意义，则x≠0，即函数的定义域是（-∞，0）∪（0，+∞），不满足条件．
    故选：A

    点评 本题主要考查函数的定义域的求解，要求熟练掌握常见函数成立的条件，比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    18．过球的一条半径的中点，作垂直于该半径的平面，则所得截面的面积是球的表面积的（　　）
    A．$\frac{3}{16}$B．$\frac{9}{16}$C．$\frac{3}{8}$D．$\frac{5}{8}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．设复数z满足（1+2i）z=1-2i，则z位于（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．若2a=5b=10，则$\frac{1}{a}$+$\frac{1}{b}$=1，lg8+2log510=$\frac{3}{a}$+2b（用a、b表示）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

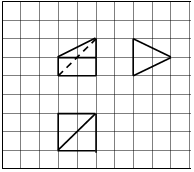    3．如图，网格纸上小正方形的边长为1，粗实线及粗虚线画出的是某多面体的三视图，则该多面体外接球的表面积为（　　）
    A．8πB．$\frac{25}{2}$πC．12πD．$\frac{41}{4}$π

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．实数x取什么值时，复数z=（x2+x-6）+（x2-2x-15）i是：①实数；②虚数；③纯虚数；④零．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

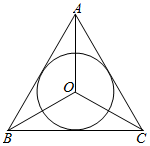    20．如图：在图O内切于正三角形△ABC，则S△ABC=S△OAB+S△OAC+S△OBC=3•S△OBC，即$\frac{1}{2}•|{BC}|•h=3•\frac{1}{2}•|{BC}|•r$，即h=3r，从而得到结论：“正三角形的高等于它的内切圆的半径的3倍”；类比该结论到正四面体，可得到结论：“正四面体的高等于它的内切球的半径的a倍”，则实数a=（　　）
    A．2B．3C．4D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．设{an}，{bn}是两个等差数列，若cn=an+bn，则{cn}也是等差数列，类比上述性质，设{sn}，{tn}是等比数列，则下列说法正确的是（　　）
    A．若rn=sn+tn，则{rn}是等比数列B．若rn=sntn，则{rn}是等比数列
    C．若rn=sn-tn，则{rn}是等比数列D．以上说明均不正确

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．在锐角△ABC中，内角A，B，C分别对应的边是a，b，c．若b2-a2=ac，则$\frac{1}{tanA}$-$\frac{1}{tanB}$的取值范围是（1，$\frac{2\sqrt{3}}{3}$）．

    查看答案和解析>>

    同步练习册答案