
| A. | ① | B. | ② | C. | ②④ | D. | ③ |
分析 分别判断两个函数的定义域和对应法则是否相同即可.
解答 解:对于①,y=$\frac{(x+3)(x-5)}{x+3}$=x-5(x≠-3),与y=x-5(x∈R)的定义域不相同,不是同一函数.
对于②,y=x2-1(x∈R),与y=$\sqrt{{{(x}^{2}-1)}^{2}}$=|x2-1|(x∈R)的对应关系不相同,不是同一函数.
对于③,y=x2-1(x∈R),与y=$\root{3}{{{(x}^{2}-1)}^{3}}$=x2-1(x∈R)的定义域和对应法则相同,是同一函数.
对于④,y=${(\sqrt{2x-5})}^{2}$=2x-5(x≥$\frac{5}{2}$),与y=2x-5(x∈R)的定义域不相同,不是同一函数.
综上,是同一函数的为③.
故选:D.
点评 本题主要考查了判断两个函数是否为同一函数的应用问题,是基础题目.


科目:高中数学 来源: 题型:解答题
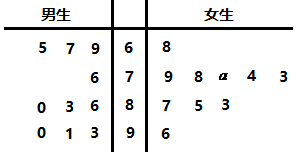 某中学为了普及法律知识,举行了一次法律知识竞赛活动.下面的茎叶图记录了男生、女生各10名学生在该次竞赛活动中的成绩(单位:分).
某中学为了普及法律知识,举行了一次法律知识竞赛活动.下面的茎叶图记录了男生、女生各10名学生在该次竞赛活动中的成绩(单位:分).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | [1,+∞) | C. | (0,2) | D. | (1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{5}$ | B. | $\frac{1}{5}$ | C. | $-\frac{3}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-0.5,-0.4) | B. | (-0.4,-0.3) | C. | (0.4,0.6) | D. | (0.8,0.9) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com