
分析 根据数列的递推公式对a进行分类讨论,分别根据递推公式求出a3、a4、a5、a6、…,归纳出数列的周期,由周期性和条件求出实数a的值.
解答 解:①当0<a<2时,
∵a1=a(a>0),a2=1,an+2=$\frac{2max\{{a}_{n+1},2\}}{{a}_{n}}$(n∈N*),
∴a3=$\frac{2max\{{a}_{2},2\}}{{a}_{1}}$=$\frac{4}{a}$,
同理可得:a4=$\frac{8}{a}$,a5=4,a6=a,a7=1,…,
可得an+5=an,数列{an}是周期为5的周期数列.
∴a2015=a5=4=4a,解得a=1,成立;
②当a≥2时,
∵a1=a(a>0),a2=1,an+2=$\frac{2max\{{a}_{n+1},2\}}{{a}_{n}}$(n∈N*),
∴a3=$\frac{2max\{{a}_{2},2\}}{{a}_{1}}$=$\frac{4}{a}$≤2,
同理可得:a4=4,a5=2a≥4,a6=a≥2,a7=1,…,
可得an+5=an,数列{an}是周期为5的周期数列,
∴a2015=a5=2a=4a,解得a=0,舍去,
综上可得,实数a的值是1,
故答案为:1.
点评 本题考查了数列递推关系的应用,数列的周期性,以及分类讨论思想,考查了推理能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{3}{95}$ | C. | $\frac{3}{19}$ | D. | $\frac{1}{95}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+25ln 5 | B. | 8+25ln $\frac{11}{3}$ | C. | 4+25ln 5 | D. | 4+50ln 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>0} | B. | {x|0<x<5} | C. | {x|x≥1} | D. | {x|1≤x<5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
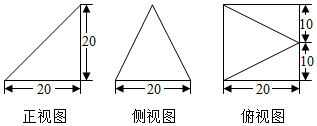
| A. | $\frac{15}{2}$cm | B. | $\frac{15}{4}$cm | C. | $\frac{5\sqrt{41}}{2}$cm | D. | $\frac{5\sqrt{41}}{4}$cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com