解:(1)由f(x)=ax
3+bx
2+cx(a≠0)为奇函数,
∴f(-x)=-f(x),代入得,b=0
∴f'(x)=3ax
2+c,且f(x)在x=1取得极大值2.
∴
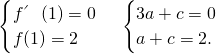
解得a=-1,c=3,
∴f(x)=-x
3+3x
(2)∵g(x)=-x
2+3+(k+1)lnx,
∴
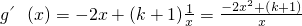
因为函数定义域为(0,+∞),所以
①当,k=-1时,g'(x)=-2x<0,函数在(0,+∞)上单调递减;
②当k<-1时,k+1<0,
∵x>0,
∴
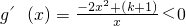
.可得函数在(0,+∞)上单调递减;
③k>-1时,k+1>0,令g'(x)>0,得
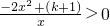
,
∵x>0,
∴-2x
2+(k+1)>0,得
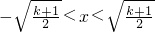
,结合x>0,得
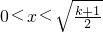
;
令g'(x)<0,得
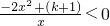
,同上得2x
2>(k+1),解得
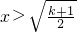
,
∴k>-1时,单调递增区间为(0,
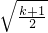
),单调递增区间为(
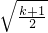
,+∞)
综上,当k≤-1时,函数的单调递减区间为(0,+∞),无单调递增区间;
当k>-1时,函数的单调递增区间为(0,
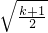
),单调递减区间为(
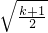
,+∞)(包含
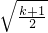
不扣分)
(3)当k=2时,g(x)=-x
2+3+3lnx,
令h(x)=g(x)-(x+m)=-x
2-x+3lnx+3-m,(11分)
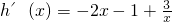
,
令h′(x)=0,
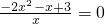
,得x=1,
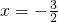
(舍去).
由函数y=h(x)定义域为(0,+∞),则当0<x<1时,h'(x)>0,
当x>1时h'(x)<0,
∴当x=1时,函数h(x)取得最大值1-m.
由1-m<0得m>1
故m的取值范围是(1,+∞).
分析:(1)根据函数为奇函数求出b,然后根据函数f(x)在x=1取得极大值2,建立a与c的方程组,解之即可求出函数y=f(x)的解析式
(2)先求函数的定义域,讨论k与-1的大小,然后利用导数的符号确定函数的单调性即可.
(3)令h(x)=g(x)-(x+m)=-x
2-x+3lnx+3-m,求出函数的导数即可.
点评:本题主要考查了函数解析式的求解,以及利用导数研究函数的单调性,考查了分类讨论的数学思想,是高考中常考的题型,属于中档题.

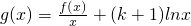 ,求函数y=g(x)的单调区间;
,求函数y=g(x)的单调区间;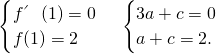
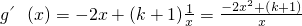
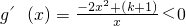 .可得函数在(0,+∞)上单调递减;
.可得函数在(0,+∞)上单调递减;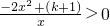 ,
,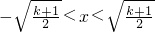 ,结合x>0,得
,结合x>0,得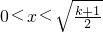 ;
;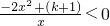 ,同上得2x2>(k+1),解得
,同上得2x2>(k+1),解得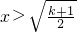 ,
,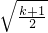 ),单调递增区间为(
),单调递增区间为(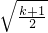 ,+∞)
,+∞)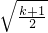 ),单调递减区间为(
),单调递减区间为(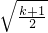 ,+∞)(包含
,+∞)(包含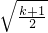 不扣分)
不扣分)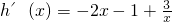 ,
,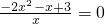 ,得x=1,
,得x=1,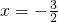 (舍去).
(舍去).
