练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

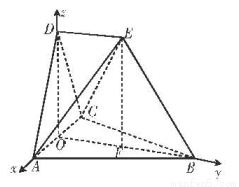
    （本题满分12分）在如图所示的空间几何体中，平面平面ABC，

    AB=BC=CA=DA=DC=BE=2，BE和平面ABC所成的角为60°，且点E在平面ABC上的射影落在

    的平分线上。

     

     

    （1）求证：DE//平面ABC；

    （2）求二面角E—BC—A的余弦值；

     

    【答案】

    解：方法一：（1）由题意知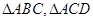， 都是边长为2的等边三角形，

    取AC中点O，连接BO，DO，

     

     

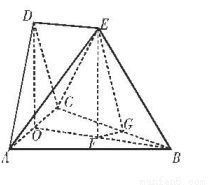
    则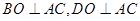

    平面ACD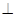平面ABC

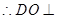    平面ABC，作EF平面ABC，

    那么EF//DO，根据题意，点F落在BO上，

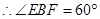    ，易求得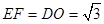

    所以四边形DEFO是平行四边形，DE//OF；

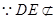    平面ABC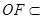，平面ABC，

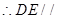    平面ABC…………6分

    （2）作FG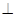BC，垂足为G，连接FG；

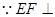    平面ABC，根据三垂线定理可知，EG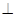BC

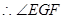    就是二面角E—BC—A的平面角

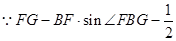
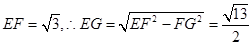
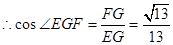
    即二面角E—BC—A的余弦值为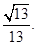…………12分

    方法二：（1）同方法一

    （2）建立如图所示的空间直角坐标系，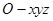

     

     

    可求得平面ABC的一个法向量为，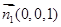

    平面BCE的一个法向量为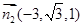

    所以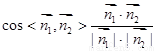

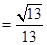
    又由图知，所求二面角的平面角是锐角，所以二面

    角E—BC—A的余弦值为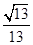；…12分

    【解析】略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （本题满分12分）

    在△ABC中，角A、B、C的对边分别为a、b、c，且．

    ??????（Ⅰ）求角A的大小；??????（Ⅱ）若，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本题满分12分）

    在平面直角坐标系中，已知A1（-3，0），A2（3，0），P（x,y），M（，0），若实数λ使向量，λ，满足λ2·（）2=·。

    （1）求点P的轨迹方程，并判断P点的轨迹是怎样的曲线；

    （2）当λ=时，过点A1且斜率为1的直线与此时（1）中的曲线相交的另一点为B，能否在直线x=-9上找一点C，使ΔA1BC为正三角形（请说明理由）。

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年辽宁沈阳二中等重点中学协作体高三领航高考预测（二）文数学卷（解析版） 题型：解答题

    （本题满分12分）在中分别为A,B,C所对的边，且

    （1）判断的形状；

    （2）若，求的取值范围

     

    查看答案和解析>>

    科目：高中数学 来源：2013届云南大理州宾川四中高二下学期4月考试文科数学试卷（解析版） 题型：解答题

    （本题满分12分）在各项为正的数列中，数列的前n项和满足

    （1）求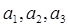；（2） 由（1）猜想数列的通项公式；（3） 求

     

    查看答案和解析>>

    科目：高中数学 来源：2013届云南省高二上学期期末考试理科数学 题型：解答题

    （本题满分12分）在边长为2的正方体中，E是BC的中点，F是的中点

    （Ⅰ）求证：CF∥平面

    （Ⅱ）求二面角的平面角的余弦值。

     

     

     

     

     

    查看答案和解析>>

    同步练习册答案