
分析 (1)当a=1时,根据函数奇偶性的定义即可判断f(x)的奇偶性;(2)根据函数单调性的定义即可证明f(x)是R上的增函数.
解答 (1)解:a=1时,f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$,
f(-x)=$\frac{{2}^{-x}-1}{{2}^{-x}+1}$=$\frac{1{-2}^{x}}{1{+2}^{x}}$=-f(x),
f(x)是奇函数;
(2)证明如下:对任意x1,x2∈R,且x1<x2,
则f(x1)-f(x2)=(a-$\frac{2}{{2}^{{x}_{1}}+1}$)-(a-$\frac{2}{{2}^{{x}_{2}}+1}$)=$\frac{2{(2}^{{x}_{1}}{-2}^{{x}_{2}})}{{(2}^{{x}_{1}}+1){(2}^{{x}_{2}}+1)}$,
∵x1<x2,
∴f(x1)-f(x2)<0,
即f(x1)<f(x2),
则函数f(x)为增函数.
点评 本题主要考查函数奇偶性和单调性的应用以及不等式恒成立问题,根据奇函数的性质,利用函数单调性和奇偶性的关系将不等式进行转化是解决本题的关键.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案科目:高中数学 来源: 题型:选择题
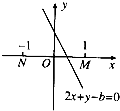
| A. | [-2,2] | B. | [-1,1] | C. | [$-\frac{1}{2},\frac{1}{2}$] | D. | [0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,1) | B. | ($\frac{3}{2}$,$\frac{9}{4}$) | C. | ($\frac{2}{3}$,$\frac{4}{9}$) | D. | (2,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1+i | B. | -1-i | C. | i | D. | -i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1<a<4 | B. | 1<a≤2 | C. | 0<a<1 | D. | 2<a<4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①②③ | D. | ①③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com