
| A. | [0,1] | B. | [-$\frac{1}{2}$,$\frac{1}{2}$] | C. | [-$\frac{\sqrt{3}}{2}$,1] | D. | [-$\frac{1}{2}$,1] |
分析 由椭圆方程可得椭圆的长轴长及焦距,再由余弦定理求得$\frac{\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}}{|P{F}_{1}||P{F}_{2}|}$的取值范围.
解答 解:由椭圆$\frac{{x}^{2}}{4}$+y2=1,得a2=4,b2=1,
∴c2=a2-b2=3,
则a=2,2a=4,c=$\sqrt{3}$,2c=2$\sqrt{3}$.
设|PF1|=m,|PF2|=n,
则m+n=2a=4,
再设∠F1PF2=θ,
则$\frac{\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}}{|P{F}_{1}||P{F}_{2}|}$=cosθ=$\frac{{m}^{2}+{n}^{2}-(2{c)}^{2}}{2mn}$=$\frac{(m+n)^{2}-2mn-12}{2mn}$
=$\frac{16-12-2mn}{2mn}=\frac{2}{mn}-1$.
∵mn$≤(\frac{m+n}{2})^{2}=4$,
∴$\frac{2}{mn}≥\frac{1}{2}$,则$\frac{2}{mn}-1≥-\frac{1}{2}$,
当P为椭圆长轴两端点时,cosθ有最大值为1.
∴$\frac{\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}}{|P{F}_{1}||P{F}_{2}|}$的取值范围为[$-\frac{1}{2},1$].
故选:D.
点评 本题主要考查椭圆定义的应用及焦点三角形问题,这类题是常考类型,考查灵活,特别是对曲线的定义和性质考查的很到位,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
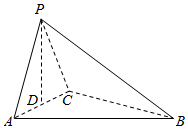 如图所示,在三棱锥P-ABC中,点P在平面ABC上的射影D与AC的中点重合,已知BC=2AC=8,AB=4$\sqrt{5}$.
如图所示,在三棱锥P-ABC中,点P在平面ABC上的射影D与AC的中点重合,已知BC=2AC=8,AB=4$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x-y+1=0 | B. | 2x-4y+2=0 | C. | 2x+4y+1=0 | D. | 2x-4y+1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{e}<m<0$ | B. | $m>-\frac{1}{e}$ | C. | m>e | D. | -e<m<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com