
分析 (Ⅰ)由题意求出a,b的值,结合隐含条件求得c,则椭圆的离心率可求;
(Ⅱ)假设存在定点N,使得以线段AB为直径的圆恒过点N,然后分直线AB的斜率存在和不存在求解,当斜率存在时,设出直线方程,与椭圆方程联立,利用根与系数的关系及AN⊥BN列式求得N的坐标;当斜率不存在时,验证AN⊥BN成立即可.
解答 解:(Ⅰ) 由椭圆方程知a2=4,${b^2}=\frac{4}{3}$,
∵a2=b2+c2,
∴$c=\frac{{2\sqrt{6}}}{3}$,则$e=\frac{c}{a}=\frac{{\sqrt{6}}}{3}$,
∴椭圆的离心率为$\frac{{\sqrt{6}}}{3}$;
(Ⅱ) 真命题.
由椭圆的对称性知,点N在x轴上,设N(t,0),
①当直线AB的斜率存在时,设其方程为y=k(x-1),
设A(x1,y1),B(x2,y2),
由$\left\{\begin{array}{l}y=k(x-1)\\{x^2}+3{y^2}=4\end{array}\right.$得,(1+3k2)x2-6k2x+3k2-4=0.
∴△=4(9k2+4)>0,
${x_1}+{x_2}=\frac{{6{k^2}}}{{1+3{k^2}}}$,${x_1}{x_2}=\frac{{3{k^2}-4}}{{1+3{k^2}}}$,
∵以线段AB为直径的圆过点N,
∴AN⊥BN,
∴$\frac{y_1}{{{x_1}-t}}×\frac{y_2}{{{x_2}-t}}=-1$,
则(x1-t)(x2-t)+y1y2=0,
∴$({x_1}-t)({x_2}-t)+{k^2}({x_1}-1)({x_2}-1)=0$,
∴$(1+{k^2}){x_1}{x_2}+({x_1}+{x_2})(-{k^2}-t)+{t^2}+{k^2}=0$,
则$(1+{k^2})\frac{{3{k^2}-4}}{{1+3{k^2}}}+\frac{{6{k^2}}}{{1+3{k^2}}}(-{k^2}-t)+{t^2}+{k^2}=0$,即-4-6tk2+t2+3t2k2=0,
∴3tk2(t-2)+(t2-4)=0,即(t-2)(3tk2+t+2)=0.
∴若以线段AB为直径的圆恒过点N(t,0),
则t-2=0,即t=2,
∴当直线AB的斜率存在时,存在N(2,0)使命题是真命题;
②当直线AB的斜率不存在时,其方程为x=1.A(1,1),B(1,-1),
以线段AB为直径的圆的方程为(x-1)2+y2=1,
∵N(2,0)满足方程(x-1)2+y2=1,
∴当直线AB的斜率不存在时,点N(2,0)也能使命题是真命题.
综上①②知,存在点N(2,0),使命题是真命题.
点评 本题考查椭圆标准方程的求法,考查了直线与圆锥曲线位置关系的应用,训练了存在性问题的求解方法,体现了分类讨论的数学思想方法,属中档题.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:选择题
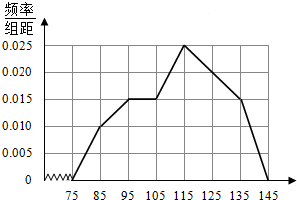 某同学将全班某次数学考试成绩整理成频率分布直方图后,并将每个小矩形上方线段的中点连接起来得到频率分布折线图(如图所示),据此估计此次考试成绩的众数是( )
某同学将全班某次数学考试成绩整理成频率分布直方图后,并将每个小矩形上方线段的中点连接起来得到频率分布折线图(如图所示),据此估计此次考试成绩的众数是( )| A. | 100 | B. | 110 | C. | 115 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | $\sqrt{13}$ | C. | 7 | D. | $\sqrt{37}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | [-$\frac{1}{2}$,$\frac{1}{2}$] | C. | [-$\frac{\sqrt{3}}{2}$,1] | D. | [-$\frac{1}{2}$,1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com