
分析 由三角函数公式化简可得f(x)=sin(2x+$\frac{π}{6}$),
(Ⅰ)由周期公式可得最小正周期,解$-\frac{π}{2}+2kπ≤2x+\frac{π}{6}≤\frac{π}{2}+2kπ$可得单调增区间;
(Ⅱ)由$x∈[0,\frac{π}{2}]$可得$2x+\frac{π}{6}∈[\frac{π}{6},\frac{7π}{6}]$,易得三角函数的最值.
解答 解:由三角函数公式化简可得$f(x)=\frac{{\sqrt{3}}}{2}sin2x+\frac{1}{2}cos2x=sin(2x+\frac{π}{6})$,
(Ⅰ)由周期公式可得函数f(x)的最小正周期$T=\frac{2π}{2}=π$,
由$-\frac{π}{2}+2kπ≤2x+\frac{π}{6}≤\frac{π}{2}+2kπ$可得$-\frac{π}{3}+kπ≤x≤\frac{π}{6}+kπ(k∈Z)$,
∴函数f(x)的单调增区间为$[-\frac{π}{3}+kπ,\frac{π}{6}+kπ](k∈Z)$;
(Ⅱ)∵$x∈[0,\frac{π}{2}]$,∴$2x+\frac{π}{6}∈[\frac{π}{6},\frac{7π}{6}]$,
∴当$2x+\frac{π}{6}=\frac{π}{2}$时,$f{(x)_{max}}=sin\frac{π}{2}=1$,
当$2x+\frac{π}{6}=\frac{7π}{6}$时,$f{(x)_{min}}=sin\frac{7π}{6}=-\frac{1}{2}$.
点评 本题考查三角函数恒等变换,涉及三角函数单调性和最值以及周期性,属基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
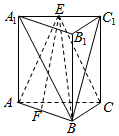 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,$A{A_1}=AC=2,AB=\sqrt{3}$,E,F分别是A1C1,AB的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,$A{A_1}=AC=2,AB=\sqrt{3}$,E,F分别是A1C1,AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{e}<m<0$ | B. | $m>-\frac{1}{e}$ | C. | m>e | D. | -e<m<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com