
分析 tanB=1,可得:B为锐角,B=$\frac{π}{4}$.由tanC=2,可得C为锐角,由$\frac{sinC}{cosC}$=2,sin2C+cos2C=1,解得sinC,cosC.利用sinA=sin(B+C)=sinBcosC+cosBsinC即可得出.再利用正弦定理可得$\frac{a}{sinA}=\frac{b}{sinB}$,即可得出.
解答 解:解法一:∵tanB=1,∴B为锐角,B=$\frac{π}{4}$.
∵tanC=2,∴C为锐角,由$\frac{sinC}{cosC}$=2,sin2C+cos2C=1,
解得sinC=$\frac{2}{\sqrt{5}}$,cosC=$\frac{1}{\sqrt{5}}$.
∴sinA=sin(B+C)=sinBcosC+cosBsinC
=$\frac{\sqrt{2}}{2}×\frac{1}{\sqrt{5}}$+$\frac{\sqrt{2}}{2}$×$\frac{2}{\sqrt{5}}$
=$\frac{3\sqrt{10}}{10}$.
∴$\frac{a}{sinA}=\frac{b}{sinB}$,
则a=$\frac{bsinA}{sinB}$=$\frac{100×\frac{3\sqrt{10}}{10}}{\frac{\sqrt{2}}{2}}$=60$\sqrt{5}$.
或解法二:tanA=-tan(B+C)=-$\frac{tanB+tanC}{1-tanBtanC}$=-$\frac{1+2}{1-1×2}$=-3,可得sinA,同解法一.
故答案为:60$\sqrt{5}$.
点评 本题考查了正弦定理、和差公式、同角三角函数基本关系式,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | ln2+1 | B. | ln2-1 | C. | ln3+1 | D. | ln3-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
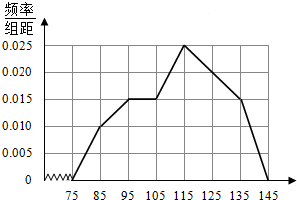 某同学将全班某次数学考试成绩整理成频率分布直方图后,并将每个小矩形上方线段的中点连接起来得到频率分布折线图(如图所示),据此估计此次考试成绩的众数是( )
某同学将全班某次数学考试成绩整理成频率分布直方图后,并将每个小矩形上方线段的中点连接起来得到频率分布折线图(如图所示),据此估计此次考试成绩的众数是( )| A. | 100 | B. | 110 | C. | 115 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{PA}$+$\overrightarrow{PB}$=$\overrightarrow{0}$ | B. | $\overrightarrow{PC}$+$\overrightarrow{PA}$=$\overrightarrow{0}$ | C. | $\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{0}$ | D. | $\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{0}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com