Question

2．已知f（x）=$\left\{{\begin{array}{l}{{x^2}+3x+1，x≥0}\\{-{x^2}+x+2，x＜0}\end{array}}\right.$，则不等式f（2x²-|x|）≤5的解集为[-1，1]．

Answer 1

分析 根据分段函数的表达式，判断函数的单调性和取值范围，结合一元二次不等式的解法进行求解即可．

解答 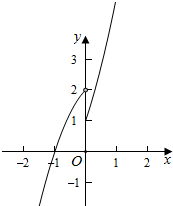解：当x＜0时，f（x）=-x²+x+2=-（x-$\frac{1}{2}$）²+$\frac{5}{4}$＜2，且函数为增函数，
当x≥0时，f（x）=x²+3x+1=-（x+$\frac{3}{2}$）²-$\frac{5}{4}$≥1，且函数为增函数，
若2x²-|x|＜0，则不等式f（2x²-|x|）≤5恒成立，
此时|x|（2|x|-1）＜0，
得0＜|x|＜$\frac{1}{2}$，
若2x²-|x|≥0，即|x|≥$\frac{1}{2}$或|x|≤0，
则不等式f（2x²-|x|）≤5恒成立，
∵f（1）=5，
∴不等式f（2x²-|x|）≤5等价为f（2x²-|x|）≤f（1），
则2x²-|x|≤1，
即2x²-|x|-1≤0，
得（|x|-1）（2|x|+1）≤0，
则|x|≤1，
∵|x|≥$\frac{1}{2}$或|x|≤0，
∴$\frac{1}{2}$≤|x|≤1或|x|=0，
综上|x|≤1，
综上-1≤x≤1，
故答案为：[-1，1]．

点评 本题主要考查不等式的求解，根据分段函数的表达式判断函数的单调性的性质，结合一元二次不等式的解法进行求解是解决本题的关键．