练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知f(x)＝x2－1，g(x)＝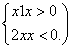

    (1)求f(g(2))和g(f(2))的值；

    (2)求f(g(x))和g(f(x))的解析式．


    解　(1)由已知，g(2)＝1，f(2)＝3，

    因此f(g(2))＝f(1)＝0，

    g(f(2))＝g(3)＝2.

    (2)当x>0时，g(x)＝x－1，

    故f(g(x))＝(x－1)2－1＝x2－2x；

    当x<0时，g(x)＝2－x，

    故f(g(x))＝(2－x)2－1＝x2－4x＋3.

    所以f(g(x))＝

    当x>1或x<－1时，f(x)>0，

    故g(f(x))＝f(x)－1＝x2－2；

    故－1<x<1时，f(x)<0，

    故g(f(x))＝2－f(x)＝3－x2.

    所以g(f(x))＝


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    点与点关于轴对称，而点与点关于原点对称，则点的坐标是（    ）

    A．　     B．     C．        D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    π是圆周率，a，b，c，d∈Q，已知命题p：若aπ＋b＝cπ＋d，则a＝c且b＝d.

    (1)写出命题p的否定并判断真假；

    (2)写出命题p的逆命题、否命题、逆否命题并判断真假；

    (3)“a＝c且b＝d”是“aπ＋b＝cπ＋d”的什么条件？并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    甲、乙、丙、丁四人在餐馆聚会，其中有一人买单，当甲的妻子询问是谁买单时，他们的回答如下．甲：不是我买的单；乙：是丁买的单；丙：是乙买的单；丁：不是我买的单．这四个人中只有一个人说了真话，由此可见，您能判定买单的人是(　　)

    A．甲                                   B．乙

    C．丙                                   D．丁

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝5|x|，g(x)＝ax2－x(a∈R)，若f[g(1)]＝1，则a＝(　　)

    A．1                                    B．2

    C．3                                    D．－1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如果对任意实数x，y，都有f(x＋y)＝f(x)·f(y)，且f(1)＝2，

    (1)求f(2)，f(3)，f(4)的值．

    (2)求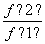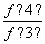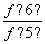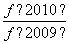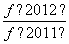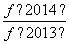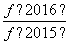＋＋＋…＋＋＋＋的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若函数f(x)＝的定义域为R，则实数m的取值范围是(　　)

    A.                               B.

    C.                                D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)＝ln(4＋3x－x2)的单调递减区间是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设集合A＝{x||x－1|<2}，B＝{y|y＝2x，x∈[0,2]}，则A∩B＝ (　　)

    A．[0,2]                                B．(1,3)

    C．[1,3)                                D．(1,4)

    查看答案和解析>>

    同步练习册答案