
【题目】如图四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() 是边长为2的等边三角形,且
是边长为2的等边三角形,且![]() ,
,![]() ,点
,点![]() 是棱
是棱![]() 上的动点.
上的动点.
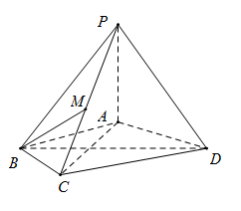
(I)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)当线段![]() 最小时,求直线
最小时,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(I)证明见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)由![]() 底面
底面![]() 可得
可得![]() .取
.取![]() 的中点
的中点![]() ,连接
,连接![]() ,根据等腰三角形的性质可得
,根据等腰三角形的性质可得![]() ,于是得到
,于是得到![]() 平面
平面![]() ,根据面面垂直的判定可得所证结论.(Ⅱ)取
,根据面面垂直的判定可得所证结论.(Ⅱ)取![]() 中点
中点![]() ,连接
,连接![]() ,可证得
,可证得![]() ,建立空间直角坐标系.然后根据向量的共线得到点
,建立空间直角坐标系.然后根据向量的共线得到点![]() 的坐标,再根据线段
的坐标,再根据线段![]() 最短得到点
最短得到点![]() 的位置,进而得到
的位置,进而得到![]() .求出平面
.求出平面![]() 的法向量后根据线面角与向量夹角间的关系可得所求.
的法向量后根据线面角与向量夹角间的关系可得所求.
(Ⅰ)证明:∵![]() 底面
底面![]() ,
,![]() 底面
底面![]() ,
,
∴![]() .
.
取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
∵![]() 是等边三角形,
是等边三角形,![]() ,
,
∴![]() ,
,![]() ,
,
∴点![]() 共线,从而得
共线,从而得![]() ,
,
又![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(Ⅱ)解:取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,
,
∴![]() 底面
底面![]() ,
,
∴![]() 两两垂直.
两两垂直.
以![]() 为原点如图建立空间直角坐标系
为原点如图建立空间直角坐标系![]() ,
,
则![]() ,
,
∴![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
由 ,得
,得![]() ,
,
令![]() ,得
,得![]() .
.
设![]() ,则
,则![]() ,
,
∴![]() ,
,
∴当![]() 时,
时,![]() 有最小值,且
有最小值,且![]() ,此时
,此时![]() .
.
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则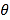 ,
,
∴直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某科研团队研发了一款快速检测某种疾病的试剂盒.为了解该试剂盒检测的准确性,质检部门从某地区(人数众多)随机选取了![]() 位患者和
位患者和![]() 位非患者,用该试剂盒分别对他们进行检测,结果如下:
位非患者,用该试剂盒分别对他们进行检测,结果如下:
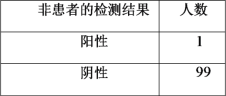
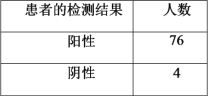
(1)从该地区患者中随机选取一人,对其检测一次,估计此患者检测结果为阳性的概率;
(2)从该地区患者中随机选取![]() 人,各检测一次,假设每位患者的检测结果相互独立,以
人,各检测一次,假设每位患者的检测结果相互独立,以![]() 表示检测结果为阳性的患者人数,利用(1)中所得概率,求
表示检测结果为阳性的患者人数,利用(1)中所得概率,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)假设该地区有![]() 万人,患病率为
万人,患病率为![]() .从该地区随机选取一人,用该试剂盒对其检测一次.若检测结果为阳性,能否判断此人患该疾病的概率超过
.从该地区随机选取一人,用该试剂盒对其检测一次.若检测结果为阳性,能否判断此人患该疾病的概率超过![]() ?并说明理由.
?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直角三角形ABC的三个顶点都在椭圆![]() 上,其中A(0,1)为直角顶点.若该三角形的面积的最大值为
上,其中A(0,1)为直角顶点.若该三角形的面积的最大值为![]() ,则实数a的值为_____.
,则实数a的值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阿基米德是古希腊伟大的哲学家、数学家、物理学家,对几何学、力学等学科作出过卓越贡献.为调查中学生对这一伟大科学家的了解程度,某调查小组随机抽取了某市的100名高中生,请他们列举阿基米德的成就,把能列举阿基米德成就不少于3项的称为“比较了解”,少于三项的称为“不太了解”.他们的调查结果如下:
0项 | 1项 | 2项 | 3项 | 4项 | 5项 | 5项以上 | |
理科生(人) | 1 | 10 | 17 | 14 | 14 | 10 | 4 |
文科生(人) | 0 | 8 | 10 | 6 | 3 | 2 | 1 |
(1)完成如下![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为,了解阿基米德与选择文理科有关?
的把握认为,了解阿基米德与选择文理科有关?
比较了解 | 不太了解 | 合计 | |
理科生 | |||
文科生 | |||
合计 |
(2)在抽取的100名高中生中,按照文理科采用分层抽样的方法抽取10人的样本.
(i)求抽取的文科生和理科生的人数;
(ii)从10人的样本中随机抽取3人,用![]() 表示这3人中文科生的人数,求
表示这3人中文科生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a![]() ,c
,c![]() ,________.(补充条件)
,________.(补充条件)
(1)求△ABC的面积;
(2)求sin(A+B).
从①b=4,②cosB![]() ,③sinA
,③sinA![]() 这三个条件中任选一个,补充在上面问题中并作答.
这三个条件中任选一个,补充在上面问题中并作答.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某贫困地区共有1500户居民,其中平原地区1050户,山区450户.为调查该地区2017年家庭收入情况,从而更好地实施“精准扶贫”,采用分层抽样的方法,收集了150户家庭2017年年收入的样本数据(单位:万元).

(1)应收集多少户山区家庭的样本数据?
(2)根据这150个样本数据,得到2017年家庭收入的频率分布直方图(如图所示),其中样本数据分组区间为(0,0.5],(0.5,1],(1,1.5],(1.5,2],(2,2.5],(2.5,3].如果将频率视为概率,估计该地区2017年家庭收入超过1.5万元的概率;
(3)样本数据中,有5户山区家庭的年收入超过2万元,请完成2017年家庭收入与地区的列联表,并判断是否有90%的把握认为“该地区2017年家庭年收入与地区有关”?
超过2万元 | 不超过2万元 | 总计 | |
平原地区 | |||
山区 | 5 | ||
总计 |
附:
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年1月22日,国新办发布消息:新型冠状病毒来源于武汉一家海鲜市场非法销售的野生动.专家通过全基因组比对发现此病毒与2003年的非典冠状病毒以及此后的中东呼吸综合征冠状病毒,分别达到70%和40%的序列相似性.这种新型冠状病毒对人们的健康生命带来了严重威胁因此,某生物疫苗研究所加紧对新型冠状病毒疫苗进行实验,并将某一型号疫苗用在动物小白鼠身上进行科研和临床实验,得到统计数据如下:
未感染病毒 | 感染病毒 | 总计 | |
未注射疫苗 | 20 |
|
|
注射疫苗 | 30 |
|
|
总计 | 50 | 50 | 100 |
现从所有试验小白鼠中任取一只,取到“注射疫苗”小白鼠的概率为![]() .
.
(1)求![]() 列联表中的数据
列联表中的数据![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)能否有99.9%把握认为注射此种疫苗对预防新型冠状病毒有效?
附:![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 过椭圆
过椭圆![]() 的右焦点,且交椭圆于A,B两点,线段AB的中点是
的右焦点,且交椭圆于A,B两点,线段AB的中点是![]() ,
,
(1)求椭圆的方程;
(2)过原点的直线l与线段AB相交(不含端点)且交椭圆于C,D两点,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥E﹣ABCD的侧棱DE与四棱锥F﹣ABCD的侧棱BF都与底面ABCD垂直,AD⊥CD,AB∥CD,AB=3,AD=4,AE=5,![]() .
.
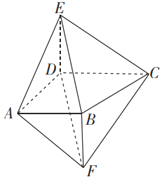
(1)证明:DF∥平面BCE.
(2)求A到平面BEDF的距离,并求四棱锥A﹣BEDF的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com