
分析 (1)根据等差数列的通项公式和求和公式求出a1,和d,即可得到数列{an}的通项公式,再根据数列的递推公式即可求出{bn}的通项公式;
(2)当n=1时求出B1,当n≥2时,利用错位相减法求数列$\left\{{\frac{b_n}{2^n}}\right\}$的前n项和Bn,验证首项后得答案.
解答 解:(1)设等差数列{an}的首项为a1,公差为d,
则由a3=7,S4=24,得$\left\{\begin{array}{l}{{a}_{1}+2d=7}\\{4{a}_{1}+\frac{4×3×d}{2}=24}\end{array}\right.$,解得a1=3,d=2.
∴an=3+2(n-1)=2n+1.
∵Tn=n2+an=n2+2n+1=(n+1)2,
当n=1时,b1=4,
当n≥2
∴Tn-1=n2,
∴bn=Tn-Tn-1=2n+1,
当n=1时,b1=3≠4,
∴bn=$\left\{\begin{array}{l}{4,n=1}\\{2n+1,n≥2}\end{array}\right.$,
(2)当n=1时,$\frac{{b}_{1}}{{2}^{1}}=\frac{4}{2}=2$;
当n≥2时,$\frac{{b}_{n}}{{2}^{n}}=\frac{2n+1}{{2}^{n}}$.
∴B1=2,
当n≥2时,${B}_{n}=2+\frac{5}{{2}^{2}}+\frac{7}{{2}^{3}}+…+\frac{2n-1}{{2}^{n-1}}+\frac{2n+1}{{2}^{n}}$,
则$\frac{1}{2}{B}_{n}=1+\frac{5}{{2}^{3}}+…+\frac{2n-1}{{2}^{n}}+\frac{2n+1}{{2}^{n+1}}$,
得$\frac{1}{2}{B}_{n}=\frac{9}{4}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{n-1}}-\frac{2n+1}{{2}^{n+1}}$=$\frac{9}{4}+\frac{\frac{1}{4}(1-\frac{1}{{2}^{n-2}})}{1-\frac{1}{2}}-\frac{2n+1}{{2}^{n+1}}$
=$\frac{9}{4}+\frac{1}{2}-\frac{1}{{2}^{n-1}}-\frac{2n+1}{{2}^{n+1}}$=$\frac{11}{4}-\frac{2n+5}{{2}^{n+1}}$.
∴${B}_{n}=\frac{11}{2}-\frac{2n+5}{{2}^{n}}$,
验证n=1时成立,
∴${B}_{n}=\frac{11}{2}-\frac{2n+5}{{2}^{n}}$.
点评 本题考查数列递推式,考查等差关系的确定,训练了错位相减法求数列的前n项和,是中档题.


科目:高中数学 来源: 题型:选择题
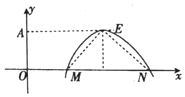 已知奇函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,点M的坐标为(1,0)且△MNE为等腰直角三角形,当A的最大值为( )
已知奇函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,点M的坐标为(1,0)且△MNE为等腰直角三角形,当A的最大值为( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{13}$ | B. | -$\frac{4}{13}$ | C. | $\frac{5}{4}$ | D. | -$\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
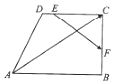 如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=3,BC=DC=2,若E,F分别是线段DC和BC上的动点,则$\overrightarrow{AC}•\overrightarrow{EF}$的取值范围是[-4,6].
如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=3,BC=DC=2,若E,F分别是线段DC和BC上的动点,则$\overrightarrow{AC}•\overrightarrow{EF}$的取值范围是[-4,6].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 圆 | B. | 两条相交直线 | C. | 球面 | D. | 抛物线 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com