
分析 (1)设所求点为(a,b),求出点到直线l的距离,利用配方法,即可得出结论;
(2)设切点分别为A(x1,y1),B(x2,y2),求出过抛物线上点A(x1,y1)的切线方程,代入x2=4y,消元,利用△=0,可得直线AB的方程,利用点到直线的距离公式求出三角形的高,即可求出三角形的面积.
解答 解:(1)设抛物线上一点N的坐标为(a,b),则b2=4a,
则点N到直线l的距离d=$\frac{|a-b+4|}{\sqrt{2}}=\frac{|\frac{{b}^{2}}{4}-b+4|}{\sqrt{2}}$=$\frac{|(\frac{b}{2}-1)^{2}+3|}{\sqrt{2}}$$≥\frac{3\sqrt{2}}{2}$,
当且仅当b=2时,等号成立,
故抛物线C上一点到直线l的最短距离为$\frac{3\sqrt{2}}{2}$.
(2)设M(t,t+4),A(x1,y1),B(x2,y2),
直线MA,MB的方程分别为x-t=m1(y-t-4),x-t=m2(y-t-4),
∵MA与抛物线有且只有一个公共点,
∴$\left\{\begin{array}{l}{x-t={m}_{1}(y-t-4)}\\{{y}^{2}=4x}\end{array}\right.$有且只有一组解,
即方程y2-4m1y+4m1t+16m1-4t=0有两个相等的实数根,
∴△=(-4m1)2-4(4m1t+16m1-4t)=0,且y1=2m1,
即m12-(t+4)m1+t=0,y1=2m1,因此A点坐标为(m12,2m1),
同理m22-(t+4)m2+t=0,y2=2m2,因此B点坐标为(m22,2m2),
由m12-(t+4)m1+t=0,m22-(t+4)m2+t=0可知,
m1,m2,是方程m2-(t+4)m+t=0的两根,
∴m1+m2=t+4,m1m2=t,
当t=-4时,直线AB的斜率为k=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=$\frac{2{m}_{2}-2{m}_{1}}{{{m}_{2}}^{2}-{{m}_{1}}^{2}}$=$\frac{2}{{m}_{1}+{m}_{2}}$,
∴直线AB的方程为y-2m1=$\frac{2}{{m}_{1}+{m}_{2}}$,(x-m12),
化简得2x-(m1+m2)y+2m1m2=0,
即2x-(t+4)y+2t=0,
当t=-4时,直线AB的方程为x=4,也符合2x-(t+4)y+2t=0,
∴点M到直线AB的距离d=$\frac{|2t-(t+4)^{2}+2t|}{\sqrt{4+(t+4)^{2}}}$=$\frac{{t}^{2}+4t+16}{\sqrt{4+(t+4)^{2}}}$
|AB|=$\sqrt{({x}_{2}-{x}_{1})^{2}+({y}_{2}-{y}_{1})^{2}}$=$\sqrt{({{m}_{1}}^{2}-{{m}_{2}}^{2})^{2}+(2{m}_{1}-2{m}_{2})^{2}}$=$\sqrt{[4+({m}_{1}+{m}_{2})^{2}]({m}_{1}-{m}_{2})^{2}}$
=$\sqrt{[4+(t+4)^{2}]({t}^{2}+4t+16)}$,
因此△MAB的面积S△MAB=$\frac{1}{2}$•$\frac{{t}^{2}+4t+16}{\sqrt{4+(t+4)^{2}}}$•$\sqrt{[4+(t+4)^{2}]({t}^{2}+4t+16)}$=$\frac{1}{2}$$•\sqrt{({t}^{2}+4t+16)^{3}}$=$\frac{1}{2}\sqrt{[(t+2)^{2}+12]^{3}}$,
故当t=-2时,△MAB的面积有最小值$12\sqrt{3}$.
点评 本题考查抛物线的切线,考查直线恒过定点,考查学生分析解决问题的能力,确定切线方程,及直线AB的方程是关键.综合性较强,运算量较大,有一定的难度.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
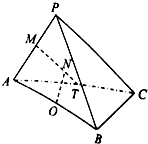 如图,在三棱锥P-ABC中,△PAC和△PBC均是边长为$\sqrt{2}$的等边三角形,AB=2,O,M,T分别是AB,PA,AC的中点.
如图,在三棱锥P-ABC中,△PAC和△PBC均是边长为$\sqrt{2}$的等边三角形,AB=2,O,M,T分别是AB,PA,AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,各个侧面均是边长为2的正方形,D为线段AC的中点.
如图,在三棱柱ABC-A1B1C1中,各个侧面均是边长为2的正方形,D为线段AC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com