Question

【题目】如图，在平面直角坐标系xOy中，已知椭圆 (a＞b＞0)的离心率为，长轴长为4.过椭圆的左顶点A作直线l，分别交椭圆和圆x2＋y2＝a2于相异两点P，Q.

(1)若直线l的斜率为，求的值；

(2)若，求实数λ的取值范围.

Answer 1

【答案】（1） （2）0＜λ＜1.

【解析】试题分析：

首先求得椭圆方程为，圆的方程为.

(1)法一：直线方程为，与椭圆方程联立可得，则，结合圆的性质可得,则.

法二：联立直线方程与椭圆方程可得： ，则.

(2)由题意可得，设直线l：y＝k(x＋2)，与椭圆方程联立可得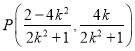，据此可得： ，同理可得，则.

试题解析：

由题意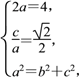得解得

所以椭圆的方程为＋＝1，圆的方程为x2＋y2＝4.

(1)法一　直线l的方程为y＝ (x＋2)，

由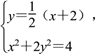得3x3＋4x－4＝0.

解得xA＝－2，xP＝，所以P.

所以AP＝＝.

又因为原点O到直线l的距离d＝＝，

所以AQ＝2＝，所以＝＝.

法二　由得3y2－4y＝0，所以yP＝.

由得5y2－8y＝0，所以yQ＝.

所以＝＝×＝.

(2)若＝λ，则λ＝－1，

设直线l：y＝k(x＋2)，

由得(2k2＋1)x2＋8k2x＋8k2－4＝0，

即(x＋2)[(2k2＋1)x＋(4k2－2)]＝0，

所以xA＝－2，xP＝，得P.

所以AP2＝＝，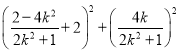

即AP＝.同理可得AQ＝.

所以λ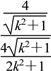＝－1＝1－.

由题意知k2＞0，所以0＜λ＜1.