
已知点集L={(x,y)|y=m·n},其中m=(2x-2b,1),n=(1,1+2b),点列Pn(an,bn)在点集L中,P1为L的轨迹与y轴的交点,已知数列{an}为等差数列,且公差为1,n∈N*.
(1)求数列{an},{bn}的通项公式;
(2)求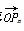 ·OPn+1的最小值;
·OPn+1的最小值;
(3)设cn=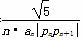 (n≥2),求c2+c3+c4+…+cn的值.
(n≥2),求c2+c3+c4+…+cn的值.
解析: (1)由y=m·n,
m=(2x-2b,1),n=(1,1+2b),得y=2x+1,
即L的轨迹方程为y=2x+1.
∵P1为L的轨迹与y轴的交点,
∴P1(0,1),则a1=0,b1=1,
∵数列{an}为等差数列,且公差为1,
∴an=n-1(n∈N*),
代入y=2x+1,得bn=2n-1(n∈N*).
(2)∵Pn(n-1,2n-1),∴Pn+1(n,2n+1),
∴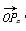 ·OPn+1=(n-1,2n-1)·(n,2n+1)
·OPn+1=(n-1,2n-1)·(n,2n+1)
=5n2-n-1=5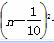 -
- .
.
∵n∈N*,
∴当n=1时,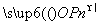 ·OPn+1有最小值,为3.
·OPn+1有最小值,为3.
(3)当n≥2时,由Pn(n-1,2n-1),
得an·|PnPn+1|= (n-1),
(n-1),
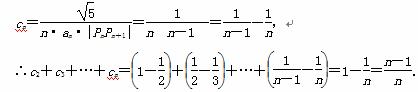


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
已知关于x的不等式|ax-1|+|ax-a|≥2(a>0).
(1) 当a=1时,求此不等式的解集;
(2) 若此不等式的解集为R,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an},{bn}满足a1=b1=3,an+1-an= =3,n∈N*,若数列{cn}满足cn=ban,则c2 013=( )
=3,n∈N*,若数列{cn}满足cn=ban,则c2 013=( )
A.92 012 B.272 012
C.92 013 D.272 013
查看答案和解析>>
科目:高中数学 来源: 题型:
已知f(x)是定义域为实数集R的偶函数,∀x1≥0,∀x2≥0,若x1≠x2,则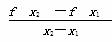 <0.如果f
<0.如果f =
=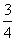 ,4f(log
,4f(log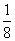 x)>3,那么x的取值范围为( )
x)>3,那么x的取值范围为( )
A. 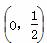 B.
B. 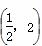
C. 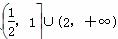 D.
D.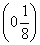 ∪
∪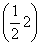
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com