
关于x的不等式x2-2ax-8a2<0(a>0)的解集为(x1,x2),且x2-x1=15,则a=( )
A.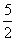 B.
B.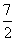
C.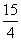 D.
D.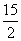
科目:高中数学 来源: 题型:
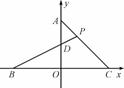
如图,已知A、B、C三点的坐标分别为(0,1)、(-1,0)、(1,0),P是线段AC上一点,BP交AO于点D,设三角形ADP的面积为S,点P的坐标为(x,y),求S关于x的函数表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
二维空间中圆的一维测度(周长)l=2πr,二维测度(面积)S=πr2,观察发现S′=l;三维空间中球的二维测度(表面积)S=4πr2,三维测度(体积)V=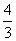 πr3,观察发现V′=S.则由四维空间中“超球”的三维测度V=8πr3,猜想其四维测度W=________.
πr3,观察发现V′=S.则由四维空间中“超球”的三维测度V=8πr3,猜想其四维测度W=________.

查看答案和解析>>
科目:高中数学 来源: 题型:
已知点集L={(x,y)|y=m·n},其中m=(2x-2b,1),n=(1,1+2b),点列Pn(an,bn)在点集L中,P1为L的轨迹与y轴的交点,已知数列{an}为等差数列,且公差为1,n∈N*.
(1)求数列{an},{bn}的通项公式;
(2)求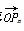 ·OPn+1的最小值;
·OPn+1的最小值;
(3)设cn=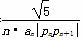 (n≥2),求c2+c3+c4+…+cn的值.
(n≥2),求c2+c3+c4+…+cn的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数y=f(x)的图象关于y轴对称,且当x∈(-∞,0)时,f(x)+xf′(x)<0成立,a=(20.2)·f(20.2),b=(logπ3)·f(logπ3),c=(log39)·f(log39),则a,b,c的大小关系是( )
A.b>a>c B.c>a>b
C.c>b>a D.a>c>b
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=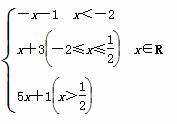 .
.
(1)求函数f(x)的最小值;
(2)已知m∈R,命题p:关于x的不等式f(x)≥m2+2m-2对任意m∈R恒成立;q:函数y=(m2-1)x是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知f(x)是定义在R上的奇函数,当0≤x≤1时,f(x)=x2,当x>0时,f(x+1)=f(x)+f(1),且.
若直线y=kx与函数y=f(x)的图象恰有5个不同的公共点,则实数k的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com