练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

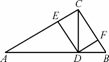
    已知：如图所示，在Rt△ABC中，∠ACB＝90°，CD⊥AB于D，DE⊥AC于E，DF⊥BC于F.求证：AE·BF·AB＝CD3.


    证明：∵ ∠ACB＝90°，CD⊥AB，

    ∴ CD2＝AD·BD，故CD4＝AD2·BD2.

    又在Rt△ADC中，DE⊥AC，

    Rt△BDC中，DF⊥BC，

    ∴ AD2＝AE·AC，BD2＝BF·BC.

    ∴ CD4＝AE·BF·AC·BC.

    ∵ AC·BC＝AB·CD，

    ∴ CD4＝AE·BF·AB·CD，即AE·BF·AB＝CD3.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如图所示，四边形ABCD和四边形AB′C′D分别是矩形和平行四边形，其中各点的坐标分别为A(－1，2)、B(3，2)、C(3，－2)、D(－1，－2)、B′(3，7)、C′(3，3)．求将四边形ABCD变成四边形AB′C′D的变换矩阵M.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知直线C1： (t为参数)，C2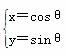： (θ为参数)．

    (1) 当α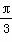＝时，求C1与C2的交点坐标；

    (2) 过坐标原点O作C1的垂线，垂足为A，P为OA中点，当α变化时，求P点的轨迹的参数方程，并指出它是什么曲线．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


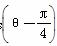    在平面直角坐标系中，以坐标原点为极点，x轴的非负半轴为极轴建立坐标系．已知点A的极坐标为，直线的极坐标方程为ρcos＝a，且点A在直线上．

    (1) 求a的值及直线的直角坐标方程；

    (2) 圆C的参数方程为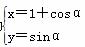，(α为参数)，试判断直线与圆的位置关系．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     如图，平行四边形ABCD中，AE∶EB＝1∶2，△AEF的面积为6，求△ADF的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


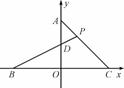
    如图，已知A、B、C三点的坐标分别为(0，1)、(－1，0)、(1，0)，P是线段AC上一点，BP交AO于点D，设三角形ADP的面积为S，点P的坐标为(x，y)，求S关于x的函数表达式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，点A，B，C是圆O上的点，且AB＝4，∠ACB＝45°，求圆O的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，正三角形ABC外接圆的半径为1，点M、N分别是边AB、AC的中点，延长MN与△ABC的外接圆交于点P，求线段NP的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知点集L＝{(x，y)|y＝m·n}，其中m＝(2x－2b,1)，n＝(1,1＋2b)，点列Pn(an，bn)在点集L中，P1为L的轨迹与y轴的交点，已知数列{an}为等差数列，且公差为1，n∈N*.

    (1)求数列{an}，{bn}的通项公式；

    (2)求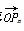·OPn＋1的最小值；

    (3)设cn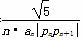＝ (n≥2)，求c2＋c3＋c4＋…＋cn的值．

    查看答案和解析>>

    同步练习册答案