
 ��֪��Բ$C��\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��a��b��0��$������Ϊ$e=\frac{{\sqrt{3}}}{2}$����ԭ��ΪԲ�ģ�����ԲC�Ķ̰��᳤Ϊ�뾶��ԲO��ֱ��l1��$y=x+\sqrt{2}$���У�
��֪��Բ$C��\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��a��b��0��$������Ϊ$e=\frac{{\sqrt{3}}}{2}$����ԭ��ΪԲ�ģ�����ԲC�Ķ̰��᳤Ϊ�뾶��ԲO��ֱ��l1��$y=x+\sqrt{2}$���У����� ��1����ֱ����Բ���У����b=1����$e=\frac{c}{a}=\frac{{\sqrt{3}}}{2}$���� $c=\frac{{\sqrt{3}}}{2}a$���ɴ��������ԲC�ķ��̣�
��2���������֪��ֱ��l2��б�ʴ����Ҳ�Ϊ0���ʿ���ֱ��l�ķ���Ϊy=kx+m��m��0����������Բ���̣��ã�1+4k2��x2+8kmx+4��m2-1��=0���ɴ����ø����б�ʽ��Τ�ﶨ�����ȱ��������ʡ��ҳ���ʽ�������֪�������������OPQ�����ȡֵ��Χ��
��� �⣺��1����ֱ��l1��$x-y+\sqrt{2}=0$��Բx2+y2=b2���У�
�ã�$d=\frac{{|0+0+\sqrt{2}|}}{{\sqrt{{1^2}+{{��-1��}^2}}}}=1=b$������2�֣�
��$e=\frac{c}{a}=\frac{{\sqrt{3}}}{2}$���� $c=\frac{{\sqrt{3}}}{2}a$������3�֣�
��a2=b2+c2����${a^2}={1^2}+\frac{3}{4}{a^2}$����a2=4������4�֣�
��ԲC�ķ���Ϊ$\frac{x^2}{4}+{y^2}=1$����5�֣�
��2���������֪��ֱ��l2��б�ʴ����Ҳ�Ϊ0���ʿ���ֱ��l�ķ���Ϊ
y=kx+m��m��0����P��x1��y1����Q��x2��y2����
��$\left\{\begin{array}{l}{y=kx+m}\\{{x}^{2}+4{y}^{2}-4=0}\end{array}\right.$����ȥy�ã�1+4k2��x2+8kmx+4��m2-1��=0������6�֣�
���=64k2m2-16��1+4k2����m2-1��=16��4k2-m2+1����0��
��x1+x2=$\frac{-8km}{1+4{k}^{2}}$��x1x2=$\frac{4��{m}^{2}-1��}{1+4{k}^{2}}$������7�֣�
��y1y2=��kx1+m����kx2+m��=k2x1x2+km��x1+x2��+m2��
��ֱ��OP��PQ��OQ��б�����γɵȱ����У�
��$\frac{{y}_{1}}{{x}_{1}}•\frac{{y}_{2}}{{x}_{2}}$=$\frac{{k}^{2}{x}_{1}{x}_{2}+km��{x}_{1}+{x}_{2}��+{m}^{2}}{{x}_{1}{x}_{2}}$=k2������8�֣�
��$\frac{-8{k}^{2}{m}^{2}}{1+4{k}^{2}}$+m2=0����m��0������k2=$\frac{1}{4}$����k=��$\frac{1}{2}$������9�֣�
�ɡ���0����ֱ��OP��OQ��б�ʴ��ڣ���0��m2��2��m2��1������10�֣�
S��OPQ=$\frac{1}{2}$|x1-x2||m|=$\sqrt{{m}^{2}��2-{m}^{2}��}$=$\sqrt{1-{{��{m^2}-1��}^2}}$������11�֣�
��S��OPQ��ȡֵ��ΧΪ��0��1��������12�֣�
���� ���⿼����Բ���̵�����������������������е��⣬����ʱҪ�������⣬ע������б�ʽ��Τ�ﶨ�����ȱ��������ʡ��ҳ���ʽ�ĺ������ã�


 �ľ�ͼ���ʱ�ȷ�ϵ�д�
�ľ�ͼ���ʱ�ȷ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
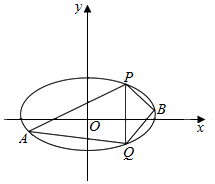 ��֪��ԲC��������ԭ�㣬������x���ϣ������ʵ���$\frac{1}{2}$������һ������˵��ǣ�0��2$\sqrt{3}$����
��֪��ԲC��������ԭ�㣬������x���ϣ������ʵ���$\frac{1}{2}$������һ������˵��ǣ�0��2$\sqrt{3}$�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{1}{2}$��ֱ��F���������߷���Ϊx=4��A��B�ֱ��������Ҷ��㣬P����Բ���������Ҷ��������һ�㣮ֱ��PA��PB����Բ�����߷ֱ���E��F���㣬����AF����Բ���ڵ�M��
��ͼ����֪��Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{1}{2}$��ֱ��F���������߷���Ϊx=4��A��B�ֱ��������Ҷ��㣬P����Բ���������Ҷ��������һ�㣮ֱ��PA��PB����Բ�����߷ֱ���E��F���㣬����AF����Բ���ڵ�M���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��$\frac{1}{3}$�� | B�� | ��0��$\frac{1}{2}$] | C�� | ��$\frac{1}{3}$��$\frac{1}{2}$] | D�� | [$\frac{1}{3}$��1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com