
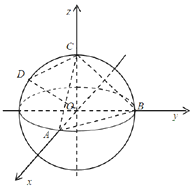
 如图所示,球O的球心O在空间直角坐标系O-xyz的原点,半径为1,且球O分别与x,y,z轴的正半轴交于A,B,C三点.已知球面上一点$D({0,-\frac{{\sqrt{3}}}{2},\frac{1}{2}})$.
如图所示,球O的球心O在空间直角坐标系O-xyz的原点,半径为1,且球O分别与x,y,z轴的正半轴交于A,B,C三点.已知球面上一点$D({0,-\frac{{\sqrt{3}}}{2},\frac{1}{2}})$.分析 (1)求出球心角,即可求D,C两点在球O上的球面距离;
(2)求出平面ABC的法向量,即可求直线CD与平面ABC所成角的大小.
解答 解:(1)由题意,cos∠COD=$\frac{\frac{1}{2}}{1×1}$=$\frac{1}{2}$,∴∠COD=$\frac{π}{3}$,
∴D,C两点在球O上的球面距离为$DC=\frac{π}{3}$;
(2)A(1,0,0),B(0,1,0),C(0,0,1),重心坐标为($\frac{1}{3}$,$\frac{1}{3}$,$\frac{1}{3}$),
∴平面ABC的法向量为$\overrightarrow{n}$=($\frac{1}{3}$,$\frac{1}{3}$,$\frac{1}{3}$),
∵$\overrightarrow{CD}$=(0,-$\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$),
∴直线CD与平面ABC所成角的正弦=|$\frac{-\frac{\sqrt{3}}{6}-\frac{1}{6}}{1•\frac{\sqrt{3}}{3}}$|=$\frac{3+\sqrt{3}}{6}$,
∴直线CD与平面ABC所成角的大小为$θ=arcsin\frac{{3+\sqrt{3}}}{6}$.
点评 本题考查球面距离,考查线面角,考查学生分析解决问题的能力,属于中档题.


 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{13}$ | C. | $\frac{\sqrt{65}}{5}$ | D. | $\sqrt{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com