
分析 (Ⅰ)函数f(x)有两个极值点等价于其导函数f'(x)在(0,+∞)有两个零点,分类讨论求实数a的取值范围;
(Ⅱ)要证${x_1}{x_2}>{e^2}$,两边同时取自然对数得$ln{x_1}+ln{x_2}>ln{e^2}=2$,由f'(x)=0得$\left\{\begin{array}{l}ln{x_1}-a{x_1}=0\\ ln{x_2}-a{x_2}=0\end{array}\right.$,得$a=\frac{{ln{x_1}+ln{x_2}}}{{{x_1}+{x_2}}}=\frac{{ln{x_1}-ln{x_2}}}{{{x_1}-{x_2}}}$.所以原命题等价于证明$ln{x_1}+ln{x_2}=\frac{{({x_1}+{x_2})(ln{x_1}-ln{x_2})}}{{{x_1}-{x_2}}}>2$.
解答 (Ⅰ)解:由题设函数f(x)的定义域为(0,+∞),f'(x)=lnx-ax,
故函数f(x)有两个极值点等价于其导函数f'(x)在(0,+∞)有两个零点.
当a=0时f'(x)=lnx,显然只有1个零点x0=1.…(2分)
当a≠0时,令h(x)=lnx-ax,那么$h'(x)=\frac{1}{x}-a=\frac{1-ax}{x}$.
若a<0,则当x>0时h'(x)>0,即h(x)单调递增,所以h(x)无两个零点.…(3分)
若a>0,则当$0<x<\frac{1}{a}$时h'(x)>0,h(x)单调递增;当$x>\frac{1}{a}$时h'(x)<0,h(x)单调递减,
所以$h(x)≤h(\frac{1}{a})=ln\frac{1}{a}-1$.
又h(1)=-a<0,当x→0时→-∞,故若有两个零点,则$h(\frac{1}{a})=ln\frac{1}{a}-1>0$,得$0<a<\frac{1}{e}$.
综上得,实数a的取值范围是$(0,\frac{1}{e})$. …(6分)
(Ⅱ)证明:要证${x_1}{x_2}>{e^2}$,两边同时取自然对数得$ln{x_1}+ln{x_2}>ln{e^2}=2$.…(7分)
由f'(x)=0得$\left\{\begin{array}{l}ln{x_1}-a{x_1}=0\\ ln{x_2}-a{x_2}=0\end{array}\right.$,得$a=\frac{{ln{x_1}+ln{x_2}}}{{{x_1}+{x_2}}}=\frac{{ln{x_1}-ln{x_2}}}{{{x_1}-{x_2}}}$.
所以原命题等价于证明$ln{x_1}+ln{x_2}=\frac{{({x_1}+{x_2})(ln{x_1}-ln{x_2})}}{{{x_1}-{x_2}}}>2$.…(8分)
因为x1<x2,故只需证$ln{x_1}-ln{x_2}<\frac{{2({x_1}-{x_2})}}{{{x_1}+{x_2}}}$,即$ln\frac{x_1}{x_2}-\frac{{2(\frac{x_1}{x_2}-1)}}{{\frac{x_1}{x_2}+1}}<0$.…(9分)
令$t=\frac{x_1}{x_2}$,则0<t<1,设$g(t)=lnt-\frac{2(t-1)}{t+1}(0<t<1)$,只需证g(t)<0.…(10分)
而$g'(t)=\frac{1}{t}-\frac{4}{{{{(t+1)}^2}}}=\frac{{{{(t-1)}^2}}}{{t{{(t+1)}^2}}}>0$,故g(t)在(0,1)单调递增,所以g(t)<g(1)=0.
综上得${x_1}{x_2}>{e^2}$.…(12分)
点评 本题考查导数知识的综合运用,考查函数的极值点,不等式的证明,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
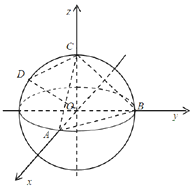 如图所示,球O的球心O在空间直角坐标系O-xyz的原点,半径为1,且球O分别与x,y,z轴的正半轴交于A,B,C三点.已知球面上一点$D({0,-\frac{{\sqrt{3}}}{2},\frac{1}{2}})$.
如图所示,球O的球心O在空间直角坐标系O-xyz的原点,半径为1,且球O分别与x,y,z轴的正半轴交于A,B,C三点.已知球面上一点$D({0,-\frac{{\sqrt{3}}}{2},\frac{1}{2}})$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 在如图所示的直角坐标系xOy中,AC⊥OB,OA⊥AB,|OB|=3,点C是OB上靠近O点的三等分点,若$y=\frac{k}{x}(x>0)$函数的图象(图中未画出)与△OAB的边界至少有2个交点,则实数k的取值范围是$0≤k<\frac{{9\sqrt{2}}}{8}$.
在如图所示的直角坐标系xOy中,AC⊥OB,OA⊥AB,|OB|=3,点C是OB上靠近O点的三等分点,若$y=\frac{k}{x}(x>0)$函数的图象(图中未画出)与△OAB的边界至少有2个交点,则实数k的取值范围是$0≤k<\frac{{9\sqrt{2}}}{8}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
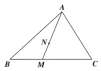 如图,在△ABC中,M为BC上不同于B,C的任意一点,点N满足$\overrightarrow{AN}=2\overrightarrow{NM}$.若$\overrightarrow{AN}=x\overrightarrow{AB}+y\overrightarrow{AC}$,则x2+9y2的最小值为$\frac{2}{5}$.
如图,在△ABC中,M为BC上不同于B,C的任意一点,点N满足$\overrightarrow{AN}=2\overrightarrow{NM}$.若$\overrightarrow{AN}=x\overrightarrow{AB}+y\overrightarrow{AC}$,则x2+9y2的最小值为$\frac{2}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 测试指标 | [85,90) | [90,95) | [95,100) | [100,105) | [105,110) |
| 机床甲 | 8 | 12 | 40 | 32 | 8 |
| 机床乙 | 7 | 18 | 40 | 29 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com