
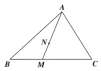
 如图,在△ABC中,M为BC上不同于B,C的任意一点,点N满足$\overrightarrow{AN}=2\overrightarrow{NM}$.若$\overrightarrow{AN}=x\overrightarrow{AB}+y\overrightarrow{AC}$,则x2+9y2的最小值为$\frac{2}{5}$.
如图,在△ABC中,M为BC上不同于B,C的任意一点,点N满足$\overrightarrow{AN}=2\overrightarrow{NM}$.若$\overrightarrow{AN}=x\overrightarrow{AB}+y\overrightarrow{AC}$,则x2+9y2的最小值为$\frac{2}{5}$. 分析 不妨设$\overrightarrow{BM}$=λ$\overrightarrow{BC}$,0<λ<1,根据向量的加减的几何意义可得x=$\frac{2-2λ}{3}$,y=$\frac{2λ}{3}$,代入得到x2+9y2=$\frac{40}{9}$(λ-$\frac{1}{10}$)2+$\frac{2}{5}$,即可求出最值.
解答 解:不妨设$\overrightarrow{BM}$=λ$\overrightarrow{BC}$,0<λ<1,
∴$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AM}$=$\frac{2}{3}$($\overrightarrow{AB}$+$\overrightarrow{BM}$)=$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{2λ}{3}$$\overrightarrow{BC}$=$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{2λ}{3}$($\overrightarrow{AC}$-$\overrightarrow{AB}$)=$\frac{2-2λ}{3}$$\overrightarrow{AB}$+$\frac{2λ}{3}$$\overrightarrow{AC}$,
∵$\overrightarrow{AN}=x\overrightarrow{AB}+y\overrightarrow{AC}$,
∴x=$\frac{2-2λ}{3}$,y=$\frac{2λ}{3}$,
∴x2+9y2=$\frac{(2-2λ)^{2}}{9}$+4λ2=$\frac{40}{9}$λ2-$\frac{8λ}{9}$+$\frac{4}{9}$=$\frac{40}{9}$(λ-$\frac{1}{10}$)2+$\frac{2}{5}$,
当λ=$\frac{1}{10}$时,x2+9y2有最小值,最小值为$\frac{2}{5}$,
故答案为:$\frac{2}{5}$.
点评 本题考查了向量的加减的几何意义以及二次函数的性质,属于中档题


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{13}$ | C. | $\frac{\sqrt{65}}{5}$ | D. | $\sqrt{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
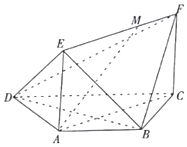 如图,在梯形ABCD中,AB∥DC,AD=AB=BC=1,$∠ADC=\frac{π}{3}$,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=1,点M在线段EF上.
如图,在梯形ABCD中,AB∥DC,AD=AB=BC=1,$∠ADC=\frac{π}{3}$,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=1,点M在线段EF上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,e] | B. | {0,e} | C. | {1,2} | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 根据“2015年国民经济和社会发展统计公报”中公布的数据,从2011 年到2015 年,我国的第三产业在GDP中的比重如下:
根据“2015年国民经济和社会发展统计公报”中公布的数据,从2011 年到2015 年,我国的第三产业在GDP中的比重如下:| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 年份代码x | 1 | 2 | 3 | 4 | 5 |
| 第三产业比重y(%) | 44.3 | 45.5 | 46.9 | 48.1 | 50.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com