
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 利用抽象函数求出函数的对称中心以及函数的周期,利用数形结合判断函数的交点个数,得到零点个数.
解答 解:由f(x)+f(2-x)=0,令x=1,则f(1)=0,
∵f(x)+f(2-x)=0,∴f(x)的图象关于点(1,0)对称,
又f(x)是定义在R上的奇函数,∴f(x)=-f(2-x)=f(x-2),
∴f(x)是周期为2的函数.
当x∈[0,1)时,f(x)=ln(ex+$\frac{x}{x+1}$)=ln(ex-$\frac{1}{x+1}$+1)为增函数,
画出f(x)及y=-$\frac{1}{3}x$在[0,6]上的图象如图所示,
经计算,结合图象易知,函数f(x)的图象与直线y=-$\frac{1}{3}x$,
在[0,6]上有3个不同的交点,由函数的奇偶性可知,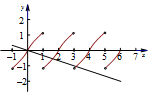
函数g(x)=f(x)+$\frac{1}{3}$x在区间[-6,6]上的零点个数是5.
故选:B.
点评 本题考查函数的零点个数的判断,抽象函数的应用,考查数形结合以及计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
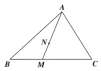 如图,在△ABC中,M为BC上不同于B,C的任意一点,点N满足$\overrightarrow{AN}=2\overrightarrow{NM}$.若$\overrightarrow{AN}=x\overrightarrow{AB}+y\overrightarrow{AC}$,则x2+9y2的最小值为$\frac{2}{5}$.
如图,在△ABC中,M为BC上不同于B,C的任意一点,点N满足$\overrightarrow{AN}=2\overrightarrow{NM}$.若$\overrightarrow{AN}=x\overrightarrow{AB}+y\overrightarrow{AC}$,则x2+9y2的最小值为$\frac{2}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 测试指标 | [85,90) | [90,95) | [95,100) | [100,105) | [105,110) |
| 机床甲 | 8 | 12 | 40 | 32 | 8 |
| 机床乙 | 7 | 18 | 40 | 29 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(1,\frac{{2+\sqrt{7}}}{3})$ | B. | $(1,\frac{{2+\sqrt{7}}}{3}]$ | C. | (1,2) | D. | (1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{7{x^2}}}{16}-\frac{y^2}{12}=1$ | B. | $\frac{y^2}{3}-\frac{x^2}{2}=1$ | C. | ${x^2}-\frac{y^2}{3}=1$ | D. | $\frac{{3{y^2}}}{23}-\frac{x^2}{23}=1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com