
| A. | $(1,\frac{{2+\sqrt{7}}}{3})$ | B. | $(1,\frac{{2+\sqrt{7}}}{3}]$ | C. | (1,2) | D. | (1,2] |
分析 利用正弦定理及双曲线的定义,可得a,c的不等式,结合PF2>c-a,即可求出双曲线的离心率的取值范围.
解答 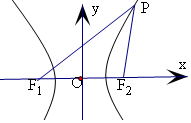 解:由$\frac{a}{{sin∠P{F_1}{F_2}}}=\frac{3c}{{sin∠P{F_2}{F_1}}}$,
解:由$\frac{a}{{sin∠P{F_1}{F_2}}}=\frac{3c}{{sin∠P{F_2}{F_1}}}$,
在△PF1F2中,由正弦定理可得
$\frac{P{F}_{2}}{sin∠P{F}_{1}{F}_{2}}$=$\frac{P{F}_{1}}{sin∠P{F}_{2}{F}_{1}}$,
可得3c•PF2=a•PF1,且PF1-PF2=2a
联立可得PF2=$\frac{2{a}^{2}}{3c-a}$>0,即得3c-a>0,即e=$\frac{c}{a}$>$\frac{1}{3}$,…①
又PF2>c-a(由P在双曲线右支上运动且异于顶点),
∴PF2=$\frac{2{a}^{2}}{3c-a}$>c-a,化简可得3c2-4ac-a2<0,
即3e2-4e-1<0,得$\frac{2-\sqrt{7}}{3}$<e<$\frac{2+\sqrt{7}}{3}$…②
又e>1,③
由①②③可得,e的范围是(1,$\frac{2+\sqrt{7}}{3}$).
故选:A.
点评 本题考查双曲线的离心率的取值范围,考查正弦定理及双曲线的定义,考查化简整理的圆能力,属于中档题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,e] | B. | {0,e} | C. | {1,2} | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
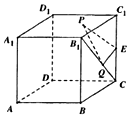 如右图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E为棱CC1的中点,点P,Q分别为面A1B1C1D1和线段B1C上的动点,则△PEQ周长的最小值为$\sqrt{10}$.
如右图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E为棱CC1的中点,点P,Q分别为面A1B1C1D1和线段B1C上的动点,则△PEQ周长的最小值为$\sqrt{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}i$ | B. | $-\frac{1}{2}i$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 根据“2015年国民经济和社会发展统计公报”中公布的数据,从2011 年到2015 年,我国的第三产业在GDP中的比重如下:
根据“2015年国民经济和社会发展统计公报”中公布的数据,从2011 年到2015 年,我国的第三产业在GDP中的比重如下:| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 年份代码x | 1 | 2 | 3 | 4 | 5 |
| 第三产业比重y(%) | 44.3 | 45.5 | 46.9 | 48.1 | 50.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com