
分析 (1)设m=1,求导数,确定函数的单调性,即可求h(x)的极值;
(2)设m<-e2,证明当$x=ln(-\frac{1}{m})$时,函数φ(x)取得最大值,最大值为$ϕ[ln(-\frac{1}{m})]=2-ln(-m)$,即可证明:函数φ(x)没有零点;
(3)x>0,F(x)>3化为(x-2)ex+x+2>0,构造函数,求导数,确定函数的单调性,即可证明结论.
解答 (1)解:∵f(x)=mex,g(x)=x+3,m=1,
∴f(x)=ex,g(x-2)=x+1,
∴h(x)=f(x)-g(x-2)-2017=ex-x-2018.
∴h'(x)=ex-1,由h'(x)=0得x=0.
∵e是自然对数的底数,∴h'(x)=ex-1是增函数.
∴当x<0时,h'(x)<0,即h(x)是减函数;
当x>0时,h'(x)>0,即h(x)是增函数.
∴函数h(x)没有极大值,只有极小值,且当x=0时,h(x)取得极小值.
∴h(x)的极小值为h(0)=-2017.
(2)证明:∵f(x)=mex,g(x)=x+3,
∴φ(x)=f(x)+g(x)=m•ex+x+3,∴φ'(x)=m•ex+1.
∵m<-e2<0,∴φ'(x)=m•ex+1是减函数.
由φ'(x)=m•ex+1=0解得$x=ln(-\frac{1}{m})$.
当$x∈(-∞,ln(-\frac{1}{m}))$时,φ'(x)=m•ex+1>0,此时函数φ(x)是增函数,
当$x∈(ln(-\frac{1}{m}),+∞)$时,φ'(x)=m•ex+1<0,此时函数φ(x)是减函数,
∴当$x=ln(-\frac{1}{m})$时,函数φ(x)取得最大值,最大值为$ϕ[ln(-\frac{1}{m})]=2-ln(-m)$.
∵m<-e2,∴2-ln(-m)<0,∴φ(x)<0,
∴当m<-e2时,函数φ(x)没有零点.
(3)证明:∵f(x)=mex,g(x)=x+3,$F(x)=\frac{m}{f(x)}+\frac{4x+4}{g(x)-1}$=$\frac{1}{{e}^{x}}$+$\frac{4x+4}{x+2}$.
∵x>0,∴F(x)>3化为(x-2)ex+x+2>0.
设u(x)=(x-2)ex+x+2,则u′(x))=(x-1)ex+1.
设v(x)=(x-1)ex+1,则v′(x)=xex.
∵x>0,∴v'(x)>0.
又∵当x=0时,v'(x)=0,∴函数v(x)在[0,+∞)上是增函数.
∵x>0,∴v(x)>v(0),即v(x)>0.
又∵x=0,v(x)=0,
∴当x>0时,u'(x)>0;当x=0时,u'(x)=0,
∴函数u(x)在[0,+∞)上是增函数.
∴当x>0时,u(x)>u(0),即$(x-2){e^{_x}}+x+2>0$.
∴当x>0时,F(x)>3.
点评 本题考查导数知识的运用,考查函数的单调性,考查不等式的证明,考查学生分析解决问题的能力,属于中档题.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(1,\frac{{2+\sqrt{7}}}{3})$ | B. | $(1,\frac{{2+\sqrt{7}}}{3}]$ | C. | (1,2) | D. | (1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
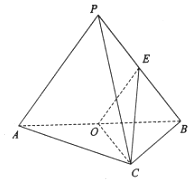 已知三棱锥P-ABC中,AC⊥BC,AC=BC=2,PA=PB=BC=3,O是AB中点,E是PB中点.
已知三棱锥P-ABC中,AC⊥BC,AC=BC=2,PA=PB=BC=3,O是AB中点,E是PB中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ①② | C. | ②③ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,1] | C. | (1,2) | D. | (1,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com