
分析 根据题意画出图形,结合图形利用$\overrightarrow{AB}$、$\overrightarrow{AD}$表示出向量$\overrightarrow{AM}$、$\overrightarrow{BD}$,计算数量积$\overrightarrow{AM}$•$\overrightarrow{BD}$即可.
解答 解:如图所示,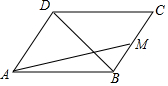
菱形ABCD中,AB=2,∠A=60°,M为BC中点,
∴$\overrightarrow{AM}$=$\overrightarrow{AB}$+$\overrightarrow{BM}$=$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{BC}$,
$\overrightarrow{BD}$=$\overrightarrow{BA}$+$\overrightarrow{AD}$=$\overrightarrow{AD}$-$\overrightarrow{AB}$,
∴$\overrightarrow{AM}$•$\overrightarrow{BD}$=($\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{BC}$)•($\overrightarrow{AD}$-$\overrightarrow{AB}$)
=$\overrightarrow{AB}$•$\overrightarrow{AD}$-${\overrightarrow{AB}}^{2}$+$\frac{1}{2}$$\overrightarrow{BC}$•$\overrightarrow{AD}$-$\frac{1}{2}$$\overrightarrow{BC}$•$\overrightarrow{AB}$
=2×2×cos60°-22+$\frac{1}{2}$×2×2×cos0°-$\frac{1}{2}$×2×2×cos60°
=-1.
故答案为:-1.
点评 本题考查了平面向量的数量积与平面向量基本定理应用问题,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | a1008>a1009 | B. | a2016<b2016 | ||
| C. | ?n∈N*,1<n<2017,an>bn | D. | ?n∈N*,1<n<2017,使得an=bn |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
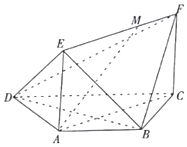 如图,在梯形ABCD中,AB∥DC,AD=AB=BC=1,$∠ADC=\frac{π}{3}$,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=1,点M在线段EF上.
如图,在梯形ABCD中,AB∥DC,AD=AB=BC=1,$∠ADC=\frac{π}{3}$,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=1,点M在线段EF上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,e] | B. | {0,e} | C. | {1,2} | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com